11.8.1 Was ist eine physikalische Grösse?
Eine physikalische Grösse ist das Produkt aus einem Zahlenwert und einer Einheit [SIA 2025]:

Wählt man eine xmal so grosse Einheit, so verkleinert sich der Zahlenwert auf den xten Teil. Das Produkt aus Zahlenwert und Einheit bleibt unverändert.
Beispiel:
Länge L = 30 cm = 0,3 m
Einheiten des internationalen Masssystems (SI)
|
Grösse |
SI-Einheit |
Name |
|
|
Länge |
m |
Meter |
|
|
Masse |
kg |
Kilogramm |
|
|
Zeit |
s |
Sekunde |
|
|
elektr. Stromstärke |
A |
Ampère |
|
|
Temperatur |
K |
Kelvin |
|
|
Lichtstärke |
cd |
Candela |
|
|
Stoffmenge |
mol |
Mol |
|
|
Kraft |
N |
= kg·m/s2 |
Newton |
|
Druck |
Pa |
= N/m2 |
Pascal |
|
Energie, Arbeit |
J |
= N·m |
Joule |
|
Leistung |
W |
= J/s |
Watt |
|
elektr. Spannung |
V |
= W/A |
Volt |
|
elektr. Widerstand |
Ω |
= V/A |
Ohm |
|
elektr. Leitwert |
S |
= 1/Ω |
Siemens |
11.8.2 Grössengleichungen
- Jedes Formelzeichen bedeutet eine physikalische Grösse.
- Grössengleichungen gelten unabhängig von den gewählten Einheiten.
- Bei der Auswertung ist für das Formelzeichen das Produkt aus Zahlenwert und Einheit einzusetzen.
- Einheiten können beliebig gekürzt und ersetzt werden (siehe Einheitengleichungen).
- Als Resultat ergeben sich ein Zahlenwert und eine Einheit.
Hinweis: Demgegenüber sind Zahlenwertgleichungen noch weit verbreitet. Bei Zahlenwertgleichungen werden unter den Formelzeichen nur Zahlenwerte verstanden, welche bestimmte Masseinheiten zwingend voraussetzen.
Beispiel:
Berechnung des (thermisch wirksamen) Volumenstroms und des Lüftungswärmeleistungsbedarfs gemäss Bild 1.24.
Gegeben: n = 0,3 h–1, Vi = 50 m3, ρ · cp = 0,32 Wh/m3 K), θi = 20 °C, θe = –8 °C
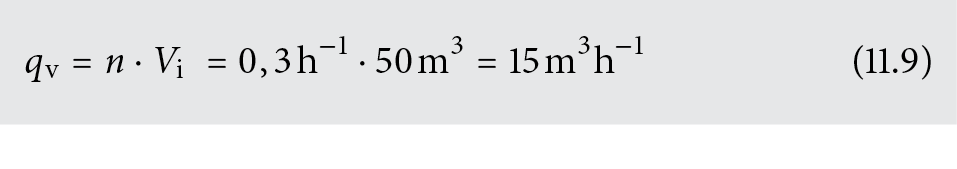
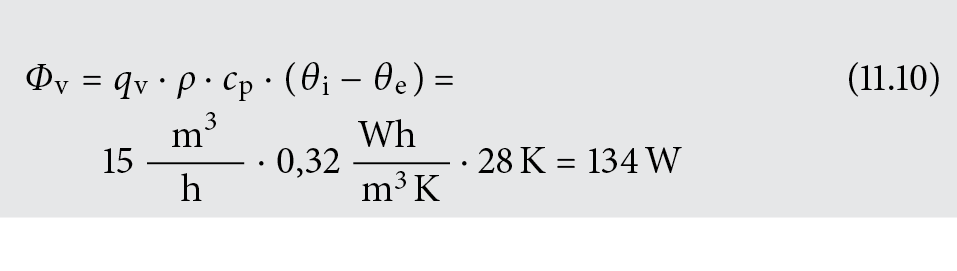
11.8.3 Einheitengleichungen
geben Beziehungen zwischen verschiedenen Einheiten an.
Beispiele:
|
Einheit |
Umrechnung |
|
|
1 in |
= 0,0254 m |
Abkürzung für inch (Zoll) |
|
1 min |
= 60 s |
|
|
1 h |
= 60 min = 3600 s |
|
|
1 d |
= 24 h = 86400 s |
|
|
1 a |
≈ 365 d |
|
|
1 bar |
= 100’000 Pa |
|
|
1 Wh |
= 3600 J = 3,6 kJ |
1 kJ = 0,278 Wh |
|
1 kWh |
= 3,6 · 106 J = 3600 kJ = 3,6 MJ |
1 MJ = 0,278 kWh |
|
1 kcal |
= 4190 J = 1,16 Wh |
|
|
1 kcal/h |
= 1,16 W |
|
|
1 PS |
= 735 W |
Vorsätze zu Einheiten
|
p = Piko |
= 0,000’000’000’001 |
= 10–12 |
|
n = Nano |
= 0,000’000’001 |
= 10 –9 |
|
μ = Mikro |
= 0,000’001 |
= 10–6 |
|
m = Milli |
= 0,001 |
= 10–3 |
|
c = Zenti |
= 0,01 |
= 10–2 |
|
d = Dezi |
= 0,1 |
= 10–1 |
|
da = Deka |
= 10 |
= 101 |
|
h = Hekto |
= 100 |
= 102 |
|
k = Kilo |
= 1’000 |
= 103 |
|
M = Mega |
= 1’000’000 |
= 106 |
|
G = Giga |
= 1’000’000’000 |
= 109 |
|
T = Tera |
= 1’000’000’000’000 |
= 1012 |
|
P = Peta |
= 1’000’000’000’000’000 |
= 1015 |
11.8.4 Ergänzende Hinweise
Druck
Der Druck wird manchmal durch die Höhe einer entsprechenden Flüssigkeitssäule dargestellt.
Beispiele:
1 mm Wassersäule (WS) bei 4 °C ![]() 9,81 Pa
9,81 Pa
1 mm Quecksilber (Hg) bei 0 °C ![]() 133,3 Pa
133,3 Pa
Die üblichen Manometer zeigen immer einen Überdruck (gegenüber Atmosphäre) an. Der Absolutdruck p ist also:

pamb Atmosphärendruck (amb = ambient), im Mittel auf Meereshöhe 1,01 bar, auf 1000 m Höhe 0,89 bar
pe Überdruck (e = excess)
Temperatur
Der Nullpunkt der Celsiusskala hat eine absolute Temperatur von 273,15 K. Für Temperaturdifferenzen sind °C und K gleichwertig.
Beispiel:
|
θ1 = 5 °C |
θ2 = 15 °C |
→ |
Δθ = 10 °C |
|
T1 = 278 K |
T2 = 288 K |
→ |
ΔT = 10 K |
Normkubikmeter
Ein DIN-Normkubikmeter [mn3] ist diejenige Gasmenge, welche bei Normbedingungen (p = 1,013 bar und θ = 0 °C) ein Volumen von 1 m3 einnimmt.
Prozent
Das Prozentzeichen (%) steht für den Faktor 10–2.
Beispiel:
Kesselwirkungsgrad gemäss Gleichung (2.13)
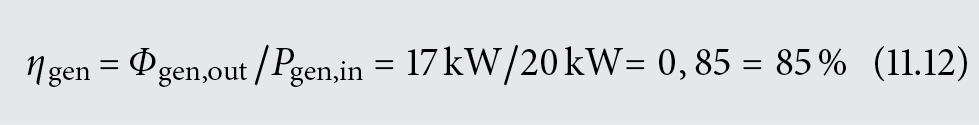
11.8.5 Übungsaufgaben zu Energie und Leistung
Wie viel Energie wird benötigt, um 200 Liter Wasser von 10 °C auf 50 °C zu erwärmen (etwa Tagesbedarf Warmwasser von 4 Personen)?
Lösung: 33,5 MJ = 9,3 kWh
Anderes Resultat? Konsultieren Sie z.B. die Gleichungen (2.23/2.24)
Wie gross ist die im Mittel erforderliche Leistung, um 200 Liter Wasser innert 24 Stunden von 10 °C auf 50 °C zu erwärmen?
Lösung: 0,39 kW
Anderes Resultat? Konsultieren Sie z.B. Gleichung (2.12).