6 Energie/Leistung

ⓘ

Die Leistungsberechnung geht im Prinzip von der Wärmestrombilanz eines einzelnen Raumes aus: Im stationären Zustand heben sich die in einen Raum eindringenden sowie im Raum erzeugten Wärmeströme und die nach aussen fliessenden Wärmeströme auf. Ein ganzes Gebäude stellt nun ein System von Räumen dar, die sich gegenseitig beeinflussen.

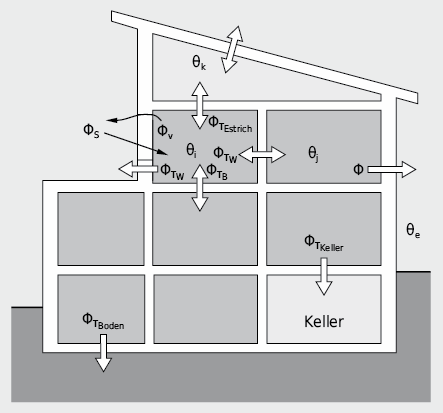
Nimmt man an, dass in einer Heizphase sämtliche Räume mit Hilfe einer Heizregelung auf festgelegten Temperaturen gehalten werden, so lässt sich die momentane Heizleistung Φ_h für jeden Raum gesondert ermitteln:

In unbeheizten Räumen ist die Heizleistung Φ_h = 0. Die Raumtemperatur wird sich so einstellen, dass das Gleichgewicht der Wärmeströme erhalten bleibt. Diese Raumtemperaturen müssen als Unbekannte in das System eingeführt werden. Bei auf vorgegebene Sollwerte beheizten Räumen stellen die verschiedenen Heizleistungen der Räume die Unbekannten dar. Die Lösung führt dann zu einem Gleichungssystem mit so vielen Unbekannten, wie Räume auftreten. Im Sommerbetrieb sind die Heizungen abgeschaltet, und alle Raumtemperaturen müssen als Variablen aufgefasst werden. Bei einer Vollklimatisierung hingegen wird man die Temperatur von Räumen oder Raumgruppen thermostatisch regeln, wobei die Raumtemperaturen wieder auf feste (Maximal-)Werte angesetzt werden können.

Zur Ermittlung des Monats- oder Jahresenergiebedarfs eines Gebäudes genügt es oft, das Gebäude als Ganzes zu betrachten und nur die Wärmeströme zu erfassen, welche die Gebäudehülle (Hüllfläche des beheizten Volumens) durchdringen. Der Wärmestrom durch Transmission und Lüftung wird dabei mit einem spezifischen Wärmetransferkoeffizienten H beschrieben (EN ISO 13789 [6.6]):

Bei der Ermittlung des Wärmetransferkoeffizienten H_T wird für jede Aussentemperaturbedingung θ_e eine Summation über die Anzahl Bauteile i, die Anzahl linienförmige Wärmebrücken k und die Anzahl punktförmige Wärmebrücken j erstellt.

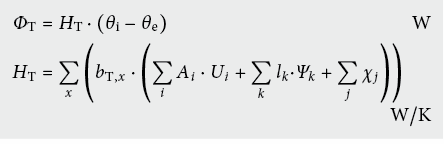
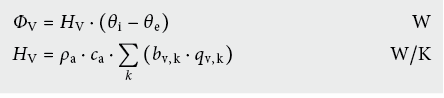
6.2.1 Detaillierte Energiebedarfsberechnung
für eine Zeitdauer Δt

Die Berechnung des Energiebedarfs erfolgt nach der Norm EN ISO 13790 [6.7].

Transmissionsverluste Q_T

Den Transmissionsverlusten durch erdberührte Bauteile ist aufgrund der ausgeprägten Mehrdimensionalität der Wärmeflüsse (Wärmebrücken), der Vielzahl der beteiligten Wärmereservoirs (Aussenluft, Innenluft, Kellerluft, Erdreich) und des grossen Wärmespeichervermögens des Erdreiches, mit den daraus resultierenden Verzögerungen seines thermischen Zustandes, besondere Beachtung zu schenken (vgl. dazu Abschnitte 2.3.6 und 6.4.2).

Lüftungsverluste Q_V

Wärmegewinne Q_g

• Personenabwärme Q_iP

• Abwärme von elektrischen Geräten Q_iEL

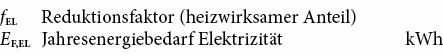
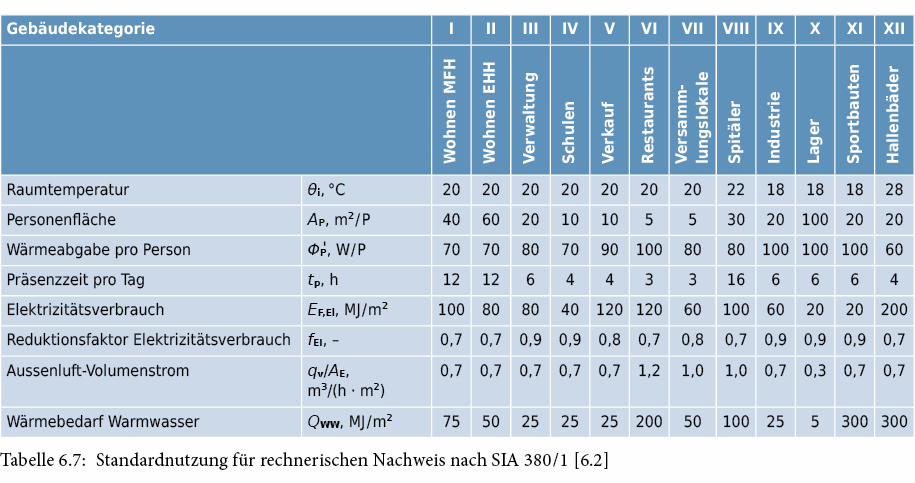
In Tab. 6.7 sind die Standardnutzungswerte, bezogen auf die Energiebezugsfläche A_E, zusammengestellt.

• Sonneneinstrahlung Q_S

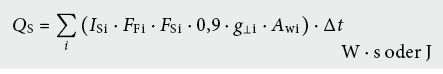
Nutzbare Wärmegewinne Q_ug

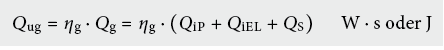
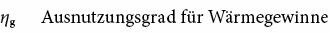
Ausnutzungsgrad η_g

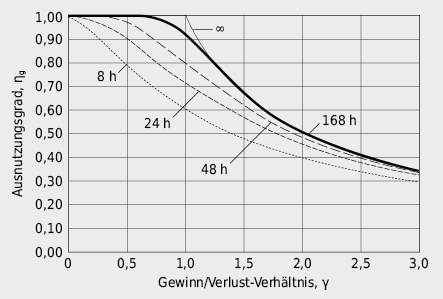
Der Ausnutzungsgrad η_g gibt an, welcher Anteil der Wärmegewinne heizwirksam ist, d. h. zu einer Verringerung des Heizwärmebedarfes führt. Der Ausnutzungsgrad für Wärmegewinne ist abhängig vom Verhältnis der Gewinne zu den Verlusten und von der thermischen Trägheit des Gebäudes. Er wird mit folgender Formel beschrieben (siehe auch Abb. 6.2):

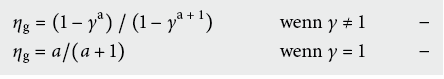
Einfluss der Wärmespeicherfähigkeit

Treibende Kraft bei der Wärmeabgabe eines Heizkörpers ist die Temperaturdifferenz zwischen Heizfläche und Raumluft. Steigt in einem Raum die Temperatur durch anfallende Wärmegewinne an, so wird die Wärmeabgabe beeinflusst, d. h., es kann ein Selbstregeleffekt beobachtet werden. Wie gross dieser ausfällt, hängt stark von der Systemtemperatur der Heizflächen ab.

Systeme mit niedrigen Vorlauftemperaturen weisen deutlich bessere Selbstregeleigenschaften auf.

Massgebend ist die effektive Wärmespeicherfähigkeit gemäss EN ISO 13786, Ziffer 7.2.2, ohne Berücksichtigung des Wärmeübergangswiderstandes R_Si für Wärmeschwankungen mit einer Periode von 24 h. Die Wärmespeicherfähigkeit wird auf die Energiebezugsfläche A_E bezogen, damit einfache Rechenwerte angegeben werden können.

Die Wärmespeicherfähigkeit dient zur Berechnung der Zeitkonstante τ = C/H. H ist der spezifische Wärmeverlust des Gebäudes (siehe Formel 6.2). C ist die Wärmespeicherfähigkeit des Raumes nach EN ISO 13786 [6.12];

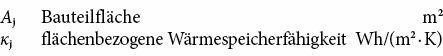
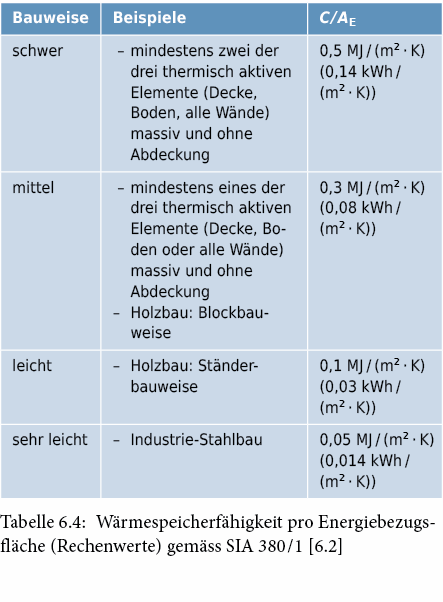
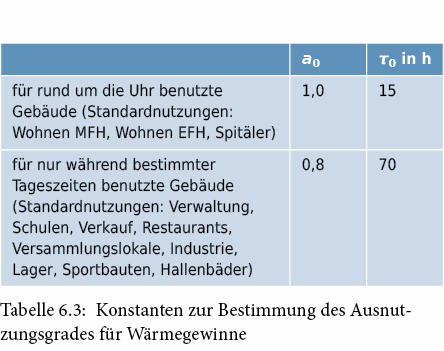
Die Zeitkonstante wird für die Berechnung des Ausnutzungsgrads für Wärmegewinne verwendet. Da dieser Ausnutzungsgrad nur relativ schwach von der Zeitkonstante abhängig ist, können für die Wärmespeicherfähigkeit pro Energiebezugsfläche C/A_E die nachstehenden angenäherten Werte in Tab. 6.4 verwendet werden.

Bei Gebäuden mit gemischter Bauweise, die mit einem Einzonenmodell berechnet werden sollen, kann ein mit der Energiebezugsfläche gewichteter Durchschnittswert der Zeitkonstante eingesetzt werden.

Die Berechnung des Heizwärmebedarfs beruht auf der Annahme einer idealen Regelung, die in allen Räumen die Raumtemperatur auf die Solltemperatur regelt und rasch auf veränderte Wärmegewinne reagiert. Ein Regelungszuschlag Δθ_i,ctr zur Raumtemperatur beschreibt den Einfluss einer nicht idealen Regelung auf den Heizwärmebedarf (siehe Tab. 6.5).

Einfluss der Heizungsregelung

Die Heizungsregelung erfolgt heute normalerweise über eine witterungsgeführte Steuerung der Vorlauftemperatur. Da in der Regel die Aussenlufttemperatur auf der Nordseite gemessen wird, erfolgt bei Sonneneinstrahlung keine Drosselung der Wärmeleistung. Eine wirksame Reaktion auf anfallende Wärmegewinne ist nur mit einer Raumtemperaturregelung möglich.

Die Verwendung von Heizkörperthermostatventilen führt bei korrekter Platzierung und Einstellung zu einer ähnlichen Wirkung wie die Raumtemperaturregelung.

Heizwärmebedarf Q_h

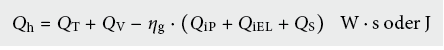
Bei der Wärmebedarfsberechnung nach SIA 380/1 werden alle Wärmemengen auf die Energiebezugsfläche A_E des Gebäudes bezogen in MJ/m².

Warmwasser Q_WW

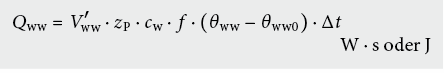
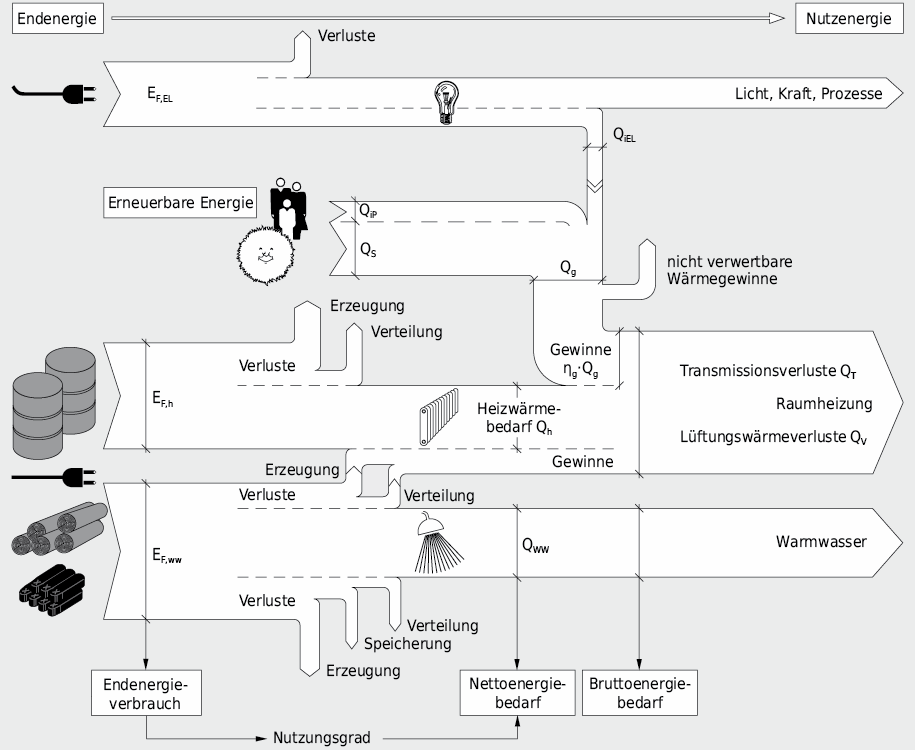
Die Energiebilanz eines Gebäudes kann anschaulich in Form eines Energieflussdiagrammes dargestellt werden. Es wird dabei zwischen End- und Nutzenergie unterschieden (vgl. Abb. 6.3).

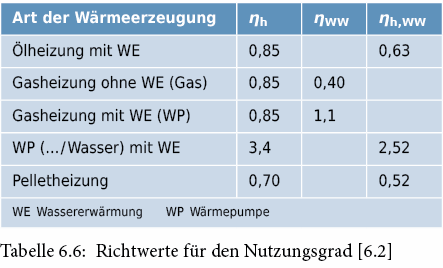
Nutzungsgrad η

Bei der Umwandlung von Endenergie zu Nutzenergie entstehen Umwandlungs- und Verteilverluste, welche mit einem sog. Nutzungsgrad berücksichtigt werden:

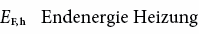
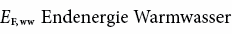
6.2.2 Heiztage und Heizgradtage ⓘ

Die Transmissions- und Lüftungswärmeverluste während einer bestimmten Zeitperiode Δt sind proportional zu (θ_i – θ_e) · Δt. Zur Berechnung des Jahresheizwärmebedarfes addiert man diese Produkte für die Dauer der Heizperiode (d. h. für die Anzahl Heiztage HT). Dabei trägt man der Tatsache Rechnung, dass die Heizung nur in Betrieb genommen wird, wenn die mittlere tägliche Aussenlufttemperatur θ _e einen bestimmten Wert, die sog. Heizgrenze θ_g, unterschreitet (vgl. [6.8]).

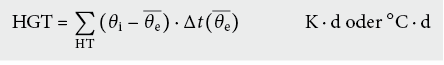
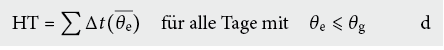
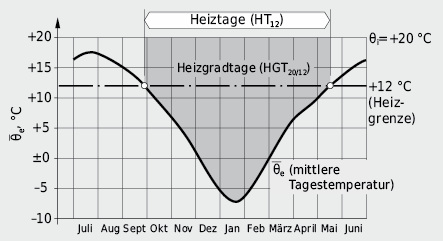
Die Heizgradtage (HGT) stellen somit eine einfache, weit verbreitete Hilfsgrösse zur Berechnung zw. Abschätzung des Energieverbrauches von beheizten Gebäuden dar. Sie entspricht der Fläche (Integral) unter der Kurve (θ_i – θ_e(t)) für alle θ_e(t) ≤ θ_g. Normalerweise wird eine Aussenlufttemperatur von θ _g = + 12 °C als Heizgrenze angenommen (→ HGT_20/12). Je nach Trägheit des Gebäudes, Wärmedämmung, Anteil freier Wärme oder spezifischer Raumnutzung können andere Grenztemperaturen angesetzt werden (z. B. passives Sonnenenergiehaus θ_g < 10 °C; leichtes Gebäude, schlecht wärmegedämmt θ _g > 12 °C; Schlafzimmer θ _i ≈ 16 °C; Bad/WC θ _i ≈ 22 °C).

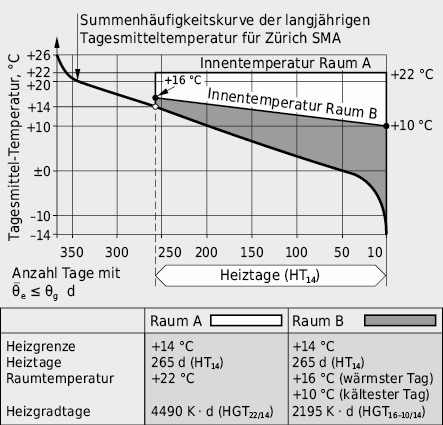
Die Anzahl der Heiztage lässt sich aber nicht nur anhand der Jahresganglinie der Aussenlufttemperatur bestimmen, sondern auch mit Hilfe der sogenannten Summenhäufigkeitskurve der mittleren täglichen Aussenlufttemperatur (siehe Anhang 9.14, 9.15). Diese Kurve gibt an, an wie vielen Tagen im Jahr eine bestimmte Temperatur unterschritten wird. Im Unterschied zur Jahresganglinie sind in der Summenhäufigkeitskurve extreme Tagesmitteltemperaturen direkt berücksichtigt. Diese Darstellung hat zudem den Vorteil, dass die Heizgradtage bei beliebiger, z. T. variabler Innenlufttemperatur und beliebiger Heizgrenze einfacher herauszulesen sind.

6.2.3 Sonnenenergiegewinn

Es können zwei Arten von Sonnenenergiegewinnen unterschieden werden:

• Direktgewinne durch Fenster
• Indirektgewinne durch besonnte, nicht transparente Bauteile (Wände, Dächer)

Während die Direktgewinne bei den Heizwärmebedarfsberechnungen berücksichtigt werden (vgl. Kap. 6.2.1), werden die Indirektgewinne häufig vernachlässigt. Besonders bei Monatsbilanzverfahren kann dies zu grösseren Fehlern bei der Transmissionswärmeverlustberechnung führen [6.23].

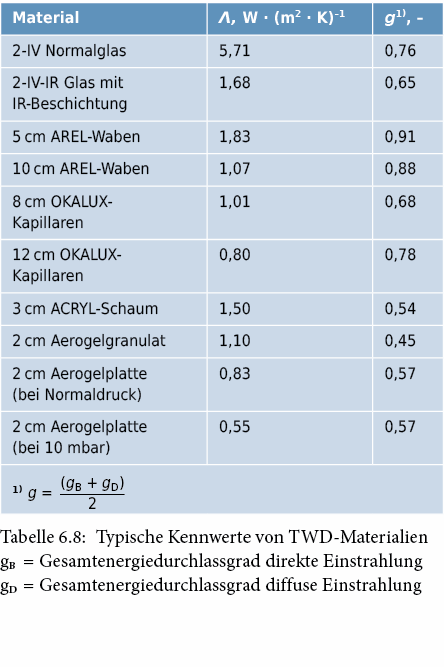
Bei Wänden mit transparenten Wärmedämmungen muss der Gewinn durch absorbierte Sonnenstrahlung erfasst werden, da er eine bedeutende Grössenordnung erreicht. Die mit einer transparenten Wärmedämmung ausgebildete Massivwand wird zu einer Kollektorwand.

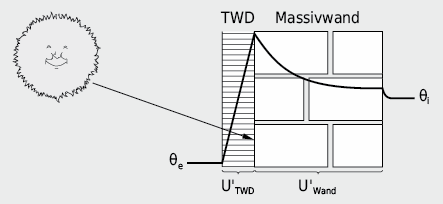
Die Sonnenstrahlung heizt die als Absorber ausgebildete Aussenwandoberfläche auf, die Wand speichert die Wärme und gibt sie verzögert an den Innenraum ab. Durch die guten Wärmedämmeigenschaften der transparenten Isolation wird nur ein geringer Anteil der gespeicherten Wärme als Verlust nach aussen weggeführt. Die Wärmebilanz einer solchen Absorberwand wird dadurch häufig positiv, d. h. die Solargewinne überwiegen die Verluste. Der Ertrag kann je nach Art des Wandsystems und der Orientierung im schweizerischen Mittelland im Bereich von (50 bis 400) MJ/m² · a liegen.

Besondere Beachtung muss dem Überhitzungsschutz dieser Absorberwände zuteil werden, können doch ohne Weiteres Absorbertemperaturen von (80–90) °C auftreten. Eine aussenliegende Sonnenschutzvorrichtung als Rouleau oder Rafflamelle ist deshalb erforderlich, um die transparente Wärmedämmung und die Wandkonstruktion im Sommer zu schützen. Die heute im Einsatz stehenden Polycarbonat-Waben oder Kapillaren lassen maximale Temperaturen von höchstens 90 °C zu.

Für die monatliche Wärmebilanzierung kann folgendes vereinfachtes Modell verwendet werden (vgl. [6.10]):

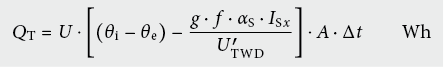
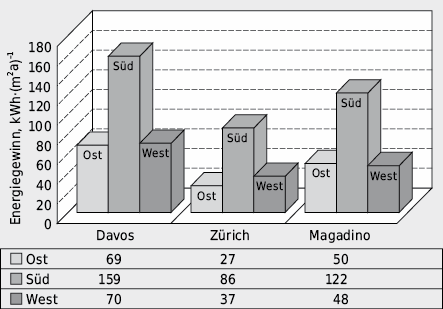
Die Energiebilanz von TWD-Fassaden ist für Ost- Süd-West-Orientierungen in der Regel positiv (vgl. Abb. 6.7).