2.1.1 Les modes de transfert de chaleur et leurs propriétés caractéristiques
L’échange de chaleur entre un système et son environnement peut se faire de différentes manières: conduction thermique, rayonnement thermique et convection.
Conduction thermique
La conduction, qui se manifeste principalement dans les corps solides et les fluides au repos, transporte de la chaleur par vibrations thermiques phonons) et mouvements des électrons libres d’un point à température plus élevée (niveau d’énergie supérieur) vers un point à plus basse température (niveau d’énergie inférieur). Elle s’opère ainsi de corpuscule en corpuscule et est liée à une différence de température. Le conducteur de chaleur demeure généralement fixe (pas de transport de masse!).
Exemple: transport de chaleur dans une barre de fer échauffée d’un seul côté.
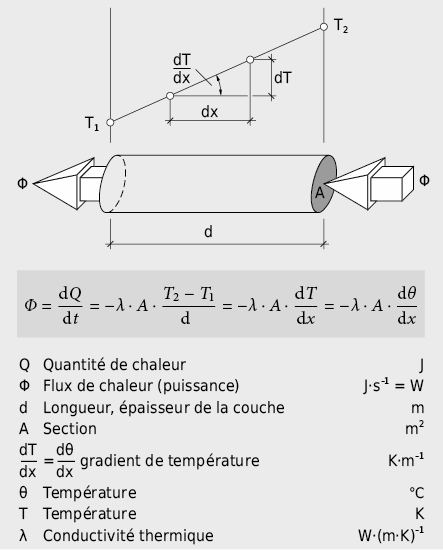
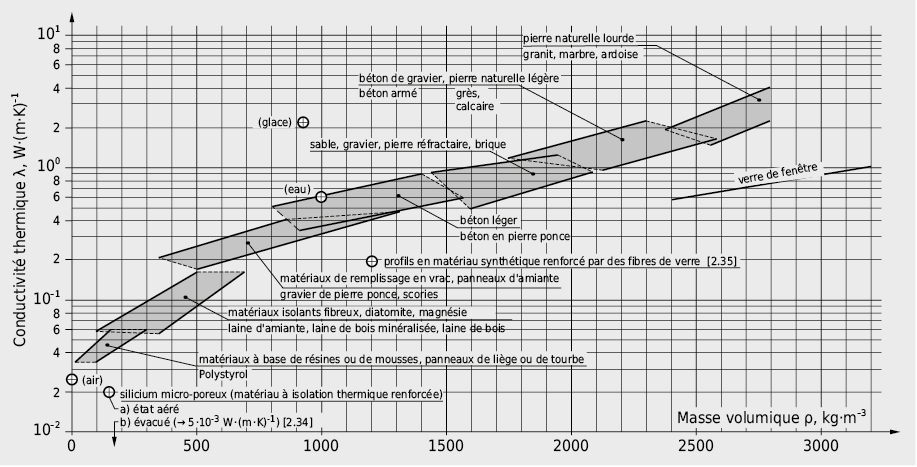
La conductivité thermique λ est une grandeur caractéristique de chaque matériau qui indique quelle quantité de chaleur s’écoule durant 1 s entre deux surfaces parallèles de 1 m2 sur une épaisseur de 1 m par une différence de température de 1 K. Elle est déterminée à partir de mesures effectuées sur des échantillons de matériau aussi homogène que possible. Les métaux purs sont généralement de bons conducteurs de chaleur. En passant des matériaux isolants aux gaz, la conductivité thermique décroît de plus en plus. Pour chaque matériau, les valeurs λ ne sont cependant pas constantes; en particulier pour les éléments de construction poreux, la composition, la densité, la structure des pores, la teneur en humidité et la température jouent un rôle déterminant. Ainsi, la conductivité thermique de ce type de matériau croît quand la porosité diminue (remplacement de l’air des pores par un matériau solide) et quand la teneur en eau augmente (remplacement de l’air des pores par de l’eau).
Plus la conductivité thermique d’un matériau est petite, meilleur est son effet d’isolation thermique.
A l’état stationnaire, le flux de chaleur par unité de surface, la densité de flux thermique q, est constante sur toute la section et se calcule comme:
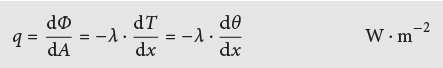
Pour les matériaux employés dans le domaine de la construction, la conductivité thermique est corrélée avec la masse volumique (voir Fig. 2.2).
Rayonnement thermique
Avec le rayonnement thermique l’énergie thermique est transportée par un rayonnement électromagnétique (aussi dans le vide) sans aucun conducteur de chaleur «matériel », c.à.d aucune masse n’est nécessaire comme support pour ce type de transfert. Le rayonnement thermique n’a pas besoin d’une différence de température agissant comme moteur. Chaque corps rayonne et ceci d’autant plus que sa température est élevée (exemples: rayonnement solaire, grill infrarouge).
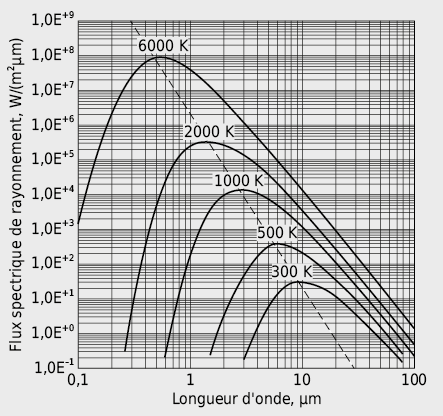
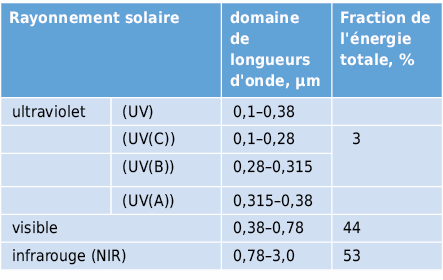
La couleur de la surface émettrice, c.à.d. la répartition des longueurs d’onde de son rayonnement, change selon sa température. Plus chaude est la source, plus courte devient la longueur d’onde du maximum du spectre et plus l’intensité du rayonnement émis augmente (puissance par unité de surface!).

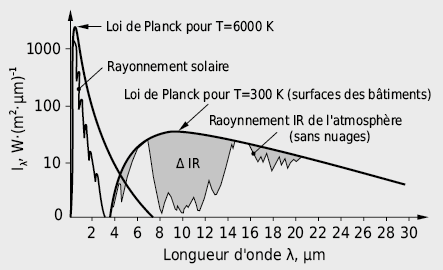
Le rayonnement de grande longueur d’onde (λ > 0,8 µm) est ressenti comme un rayonnement de chaleur (infrarouge) alors que le rayonnement de petite longueur d’onde (0,4 µm < λ < 0,8 µm) est perçu comme lumière visible. Ainsi, le soleil (température de surface Ts ≈ 6000 K) rayonne principalement entre 0,2 et 3 µm, alors que le rayonnement thermique des surfaces de murs (température de surface Ts ≈ 300 K) se situe complètement dans le domaine invisible des grandes longueurs d’onde (λ > 3 µm).
En plus de l’aire A de l’émetteur et de sa température de surface Ts (en K), le pouvoir de rayonnement (→ émissivité ε) du matériau de surface influence particulièrement le flux thermique Φ émis:

Les pertes de chaleur par rayonnement d’une surface sont d’autant plus grandes que son émissivité et sa température sont élevées.
Le transfert de chaleur par rayonnement entre surfaces est principalement déterminé par:
- les températures des surfaces (Ts (en K))
- les caractéristiques de rayonnement des surfaces (α, ε, ρ)
- la disposition des surfaces l’une par rapport à l’autre (facteur de forme Fjn)
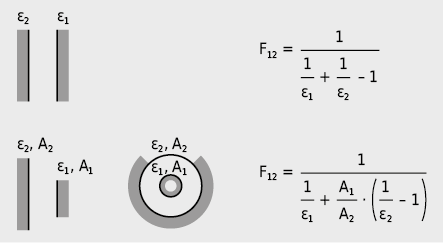
Quand deux surfaces se font face, l’échange de rayonnement peut être simplement décrit de la façon suivante (voir aussi Annexe 9.7.4):

Pour F12 = 1, ε1 = ε2 = 1 on utilise souvent une approximation linéaire:

Pour des dispositions typiques, les facteurs de forme peuvent être calculés par:
Les corps ayant une émissivité ε = 1 sont dénommés corps noirs. Les corps avec ε < 1 sont quant à eux dénommés corps gris. Le rayonnement peut aussi être partiellement ou totalement absorbé (absorption) ou transmis (transmission).
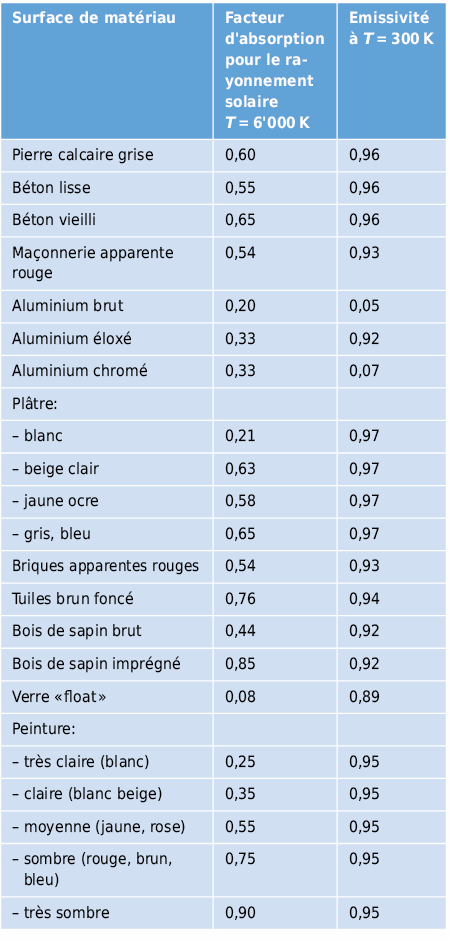
Ces paramètres caractéristiques du rayonnement sont nettement dépendant tant de la température que de la longueur d’onde. Pour une longueur d’onde λ et une température Ts déterminées on a:

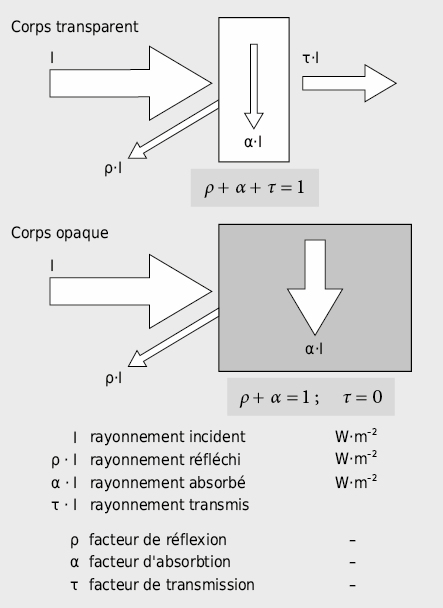
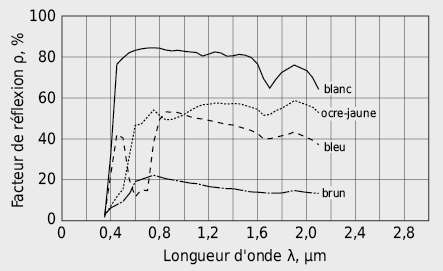
Dans les domaines spectraux importants pour la physique du bâtiment – rayonnement solaire au niveau du sol (0,3–3 µm) et rayonnement thermique (1–50 µm) – et pour des températures déterminées on peut établir des valeurs moyennes de ces paramètres valables pour les plages de longueur d’onde correspondantes:
Le mur d’un bâtiment reçoit de la chaleur d’une part du rayonnement solaire incident – tant direct que diffus (λ = 0,3–3 µm) – et, du rayonnement infrarouge de l’atmosphère (λ ≈ 3–100 µm) d’autre part. La surface d’un bâtiment de son côté rayonne, selon la loi de Stefan-Boltzmann, une puissance proportionnelle à la puissance quatre de sa température de surface Ts. Ainsi, par une nuit claire en hiver, le bilan de rayonnement de surfaces d’enveloppe fortement rayonnantes (émissivité élevée) peut devenir déficitaire. Ceci provoque – en particulier sur des toitures plates – un refroidissement de plusieurs degrés en dessous de la température de l’air (augmentation des déperditions thermiques [2.1]).
Convection
Avec la convection qui ne se produit que dans les gaz ou les liquides, la chaleur est transportée par des processus de déplacement de matière qui ont pour origine des forces internes ou externes.
Exemples: transport de chaleur dans la mer ou dans l’atmosphère, chauffage d’un local, courants thermiques (vol à voile).
Parmi les forces qui agissent sur les mouvements d’air on distingue:
- Convection naturelle, écoulement laminaire ou turbulent induit par les forces d’ascension thermique à pression constante (variation de densité)
- Convection forcée, écoulement principalement turbulent induit par une différence de pression «d’origine mécanique» (par exemple la pression du vent)
Le transfert de chaleur par convection entre surfaces est principalement influencé par les paramètres suivants:
- différence de température entre la surface θs et l’air θa (Δθ)
- vitesse d’écoulement de l’air (v)
- type d’écoulement: laminaire/turbulent (→ nombre de Reynolds Re)
- direction du flux de chaleur (horizontal, vertical vers le haut ou vers le bas)
- état de la surface (rugosité)
- température moyenne de l’air (θa)
- géométrie et dimensions des éléments (coins, niches etc.)
Le flux thermique convectif qui se produit à l’interface entre une surface solide et un gaz peut, en première approximation et malgré des relations complexes, se calculer par linéarisation de façon analogue à la conduction:
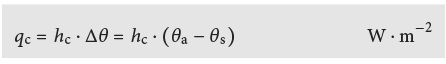
On peut employer les formules suivantes pour la détermination de hc en W · (m2 · K)–1 :
– Surfaces intérieures:
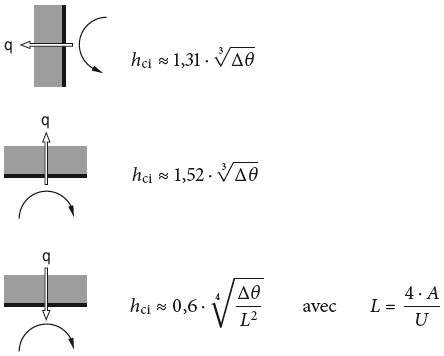
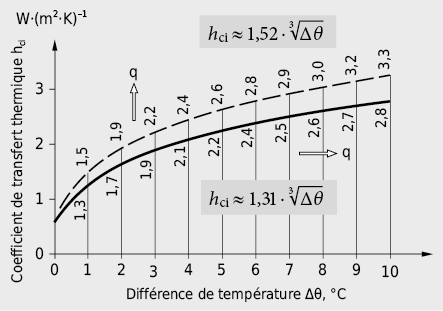
Selon la norme EN ISO 6946 [2.3] les valeurs indicatives suivantes doivent être employées en section:
- Flux de chaleur vers le haut hci = 5,0 W/(m2 K)
- Flux de chaleur horizontal hci = 2,5 W/(m2 K)
- Flux de chaleur vers le bas hci = 0,7 W/(m2 K)
– Surface extérieure:
hce = 4,0 + 4 · v
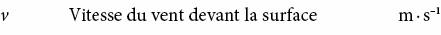
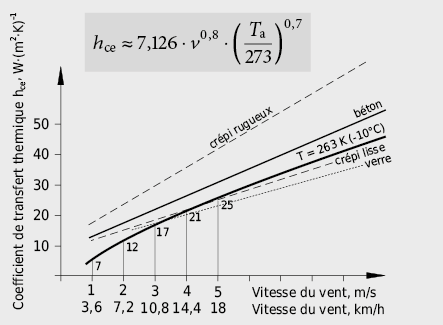
2.1.2 Données sur les matériaux de construction et facteurs d’influence
Les propriétés thermiques d’un matériau de construction doivent être obtenues par une procédure unique (par exemple EN ISO 10456 [2.4]). Dans ce contexte les désignations suivantes sont utilisées:
- Valeur mesurée, déterminée sous des conditions d’essai définies concernant la température, le taux d’humidité et l’état de vieillissement
- Valeur nominale, déterminée par une évaluation statistique des valeurs mesurées (quantile à 90 %, intervalle de confiance à 90 %) dans des conditions de références (10 °C, 50 % d’humidité relative, vieilli)
- Valeur utile (valeur de calcul), admise comme typique pour un produit dans son état installé
La conversion de la conductivité thermique d’une condition aux limites 1 vers une condition aux limites 2 s’opère selon ISO 10456 à l’aide des relations suivantes:

- Conversion pour la température

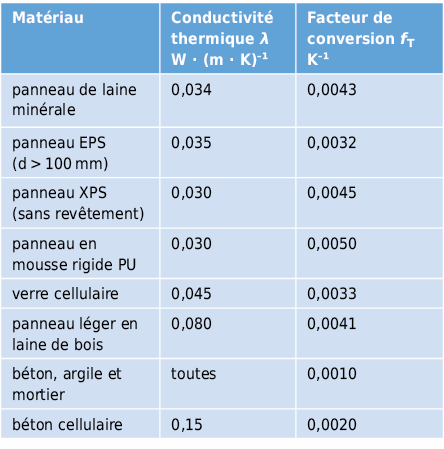
- Conversion pour le taux d’humidité
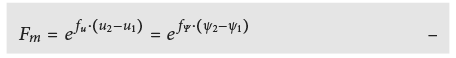
avec:

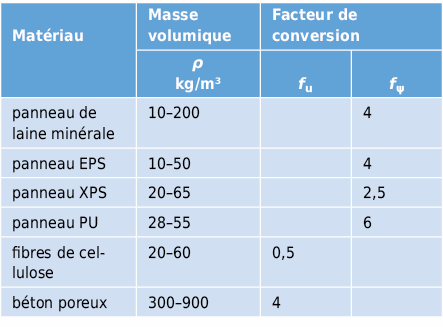
2.1.3 Transfert de chaleur entre surface de matériau et air
L’échange de chaleur entre une surface et l’air environnant peut être caractérisé à l’aide d’un coefficient de transfert de chaleur surfacique combiné (rayonnement et convection).

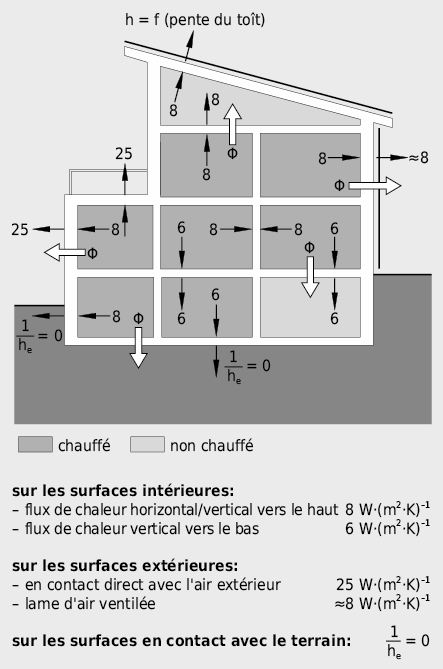
On distingue les cas suivants pour les calculs énergétiques (Fig. 2.10).
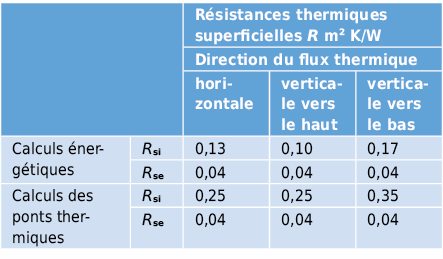
Pour les calculs énergétiques et pour l’évaluation de températures (calculs de ponts thermiques), les résistances thermiques superficielles du tableau 2.6 doivent être employées:
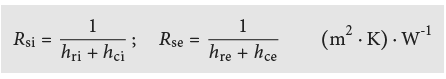
2.1.4 Résistance thermique des lames d’air
Les lames d’air disposées à l’intérieur d’éléments de construction, en particulier dans les vitrages et les cadres de fenêtres, peuvent être ordonnées selon leurs résistances thermiques ou leurs conductivités thermiques équivalentes. La part de chaque mode de tranfert de chaleur varie beaucoup selon l’épaisseur des lames et les caractéristiques de rayonnement des surfaces qui les délimitent:
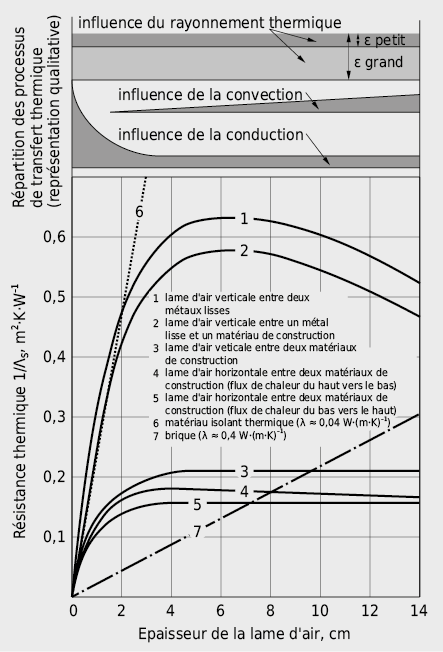
On distingue principalement les types suivants de cavités d’air d’après leurs géométries:
- A Lames d’air délimitées des deux côtés par des plans parallèles (d<< b)
- B Cavités d’air de formes rectangulaires (b/d < 10)
- C Cavités d’air de formes quelconques dans les profils de cadres de fenêtres
Lames d’air immobiles
Une lame d’air est considérée comme immobile quand sa cavité est fermée par rapport à l’environnement immédiat.
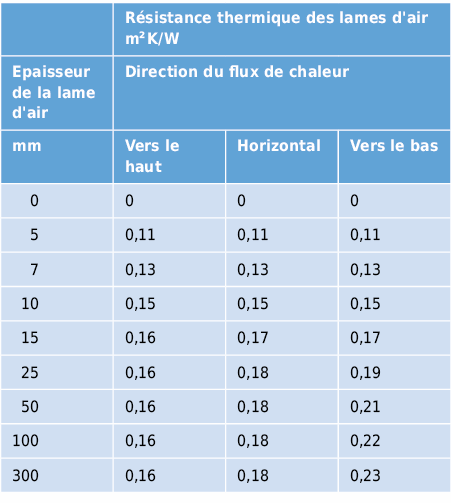
Pour des lames d’air fermées du type A avec des surfaces non metalliques, les résistances thermiques R sont indiquées au tableau 2.7 selon EN ISO 6946 [2.3].
-
des valeurs intermédiaires peuvent être interpolées
-
les lames d’air dont l’épaisseur est > 300 mm doivent être considérées comme des pièces (un bilan des flux thermiques analogue à celui d’une zone tampon doit être considéré, voir chapitre 6.3)
Pour les vitrages, le coefficient de transfert thermique Λs de l’espace entre les deux verres peut être déterminé selon EN 673 [2.12]:

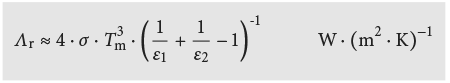
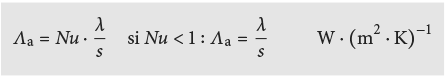




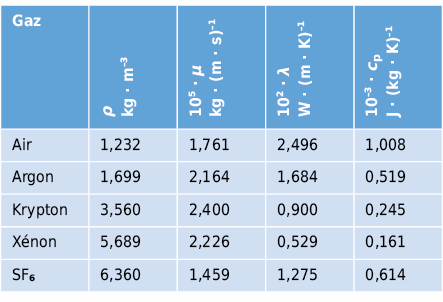
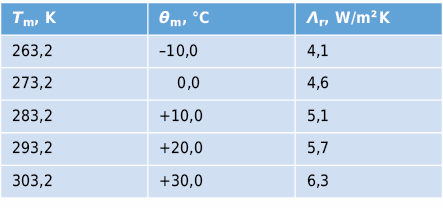
Pour des cavités fermées de type B illustrées à la Fig. 2.12, la résistance de la couche d’air ou sa conductivité thermique équivalente λeq peuvent être déterminées selon EN ISO 6946 [2.3] comme suit:
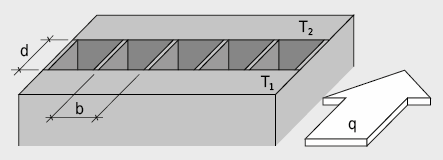
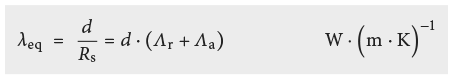
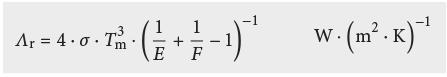

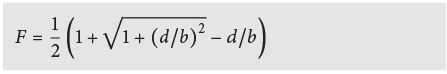
Pour ε1 = ε2 = 0,9 et Tm = 283 K on a:

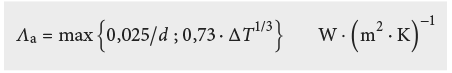
Pour des cavités d’air de type C, la forme de la section est transformée en un rectangle équivalent selon EN ISO 10077 – 2 [2.8] en conservant l’aire et le rapport d’aspect. La résistance thermique est finalement déterminée de façon analogue au type B.
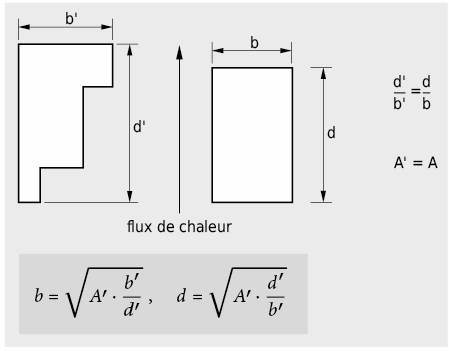
Dans les calculs de ponts thermiques, on utilise généralement la conductivité équivalente λeq de la lame d’air au lieu de sa résistance thermique (voir Tab. 2.9).
Lames d’air faiblement ventilées
Une lame d’air est faiblement ventilée quand ses échanges d’air avec l’environnement extérieur se produisent par des ouvertures limitées aux dimensions suivantes:
- > 500 mm2 à ≤ 1500 mm2 par m de longueur pour les lames d’air verticales
- > 500 mm2 à ≤ 1500 mm2 par m2 de surface pour les lames d’air horizontales
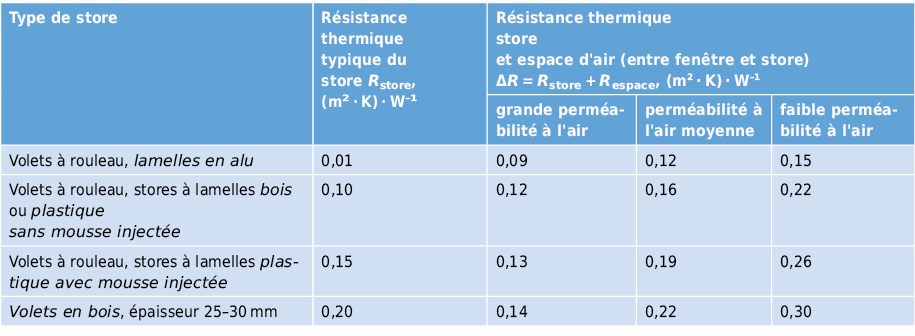
La résistance thermique d’une lame d’air faiblement ventilée correspond approximativement à la moitié de celle d’une lame d’air immobile de même épaisseur.
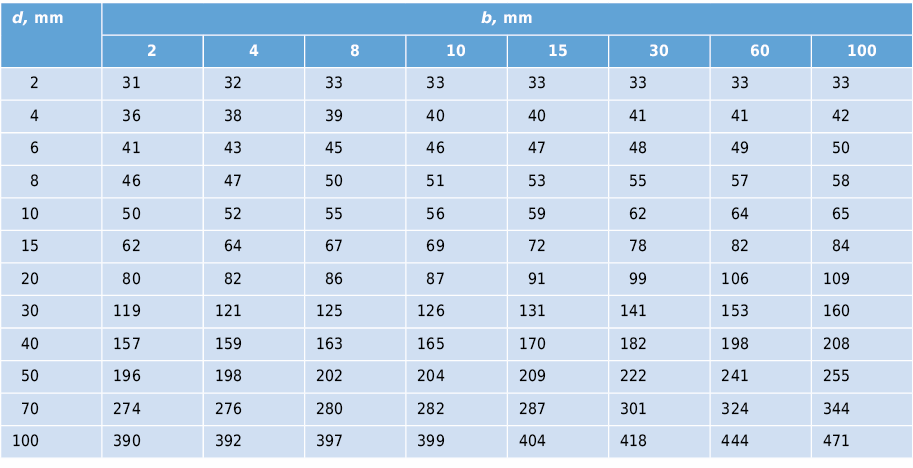
(ε1 = ε2 = 0,9, Tm = 283 K, Δθ = 10 °C)
Lames d’air fortement ventilées
Une lame d’air est considérée comme fortement ventilée quand les ouvertures entre la lame d’air et l’environnement extérieur dépasse 1500 mm2 pour chaque m de longueur ou chaque m2 de surface. Pour les lames d’air fortement ventilées, la résistance thermique superficielle extérieure (lame d’air ainsi que toutes les couches depuis la lame jusqu’à l’extérieur) peut être remplacée par la résistance thermique superficielle intérieure du même élément (voir lame d’air ventilée à la Fig. 2.10).
2.1.5 Transmission thermique et répartition de la température
Le transfert de chaleur à travers un élément de mur, de plancher ou de toiture est caractérisé par deux mécanismes fondamentaux de transport:
- transmission thermique à travers les différentes couches de matériaux: conduction de chaleur
- tansfert de chaleur à l’interface entre surface de l’élément et air: rayonnement thermique, convection et conduction
A l’état stationnaire (c’est-à-dire lorsque les températures à l’intérieur et à l’extérieur demeurent constantes), le flux de chaleur Ф est constant et s’écoule entre les surfaces de l’élément perpendiculairement à la section. Le matériau d’une couche j présente une résistance thermique dj/λj au flux de chaleur induit par la différence de température qui existe entre les deux faces de cette couche:

Comme pour le courant électrique, le flux de chaleur s’écoule dans les résistances placées en série (Δϕel = (Rel1 + Rel2 + … Reln) · I). Le flux de chaleur est déterminé par la résistance totale 1/ΛCM = Σdj/λj de toutes les couches de matériau (CM) composant l’élément:
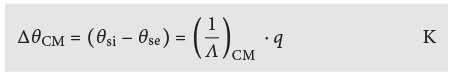
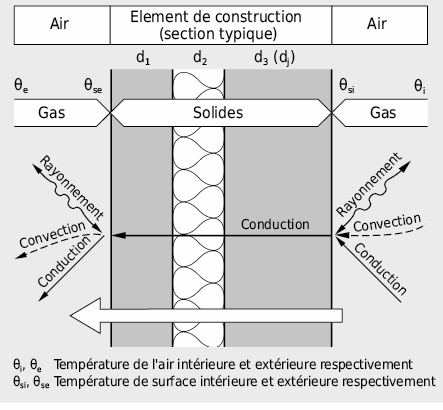
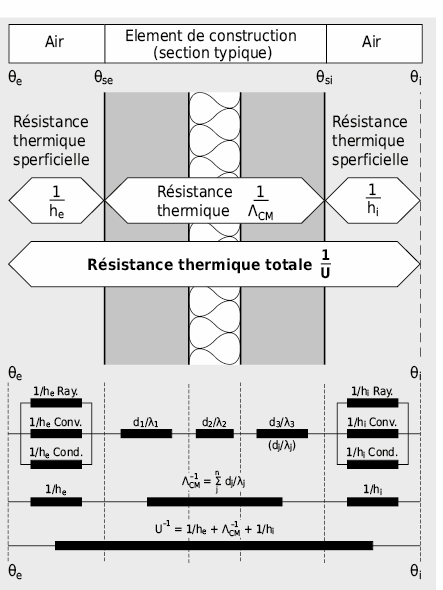
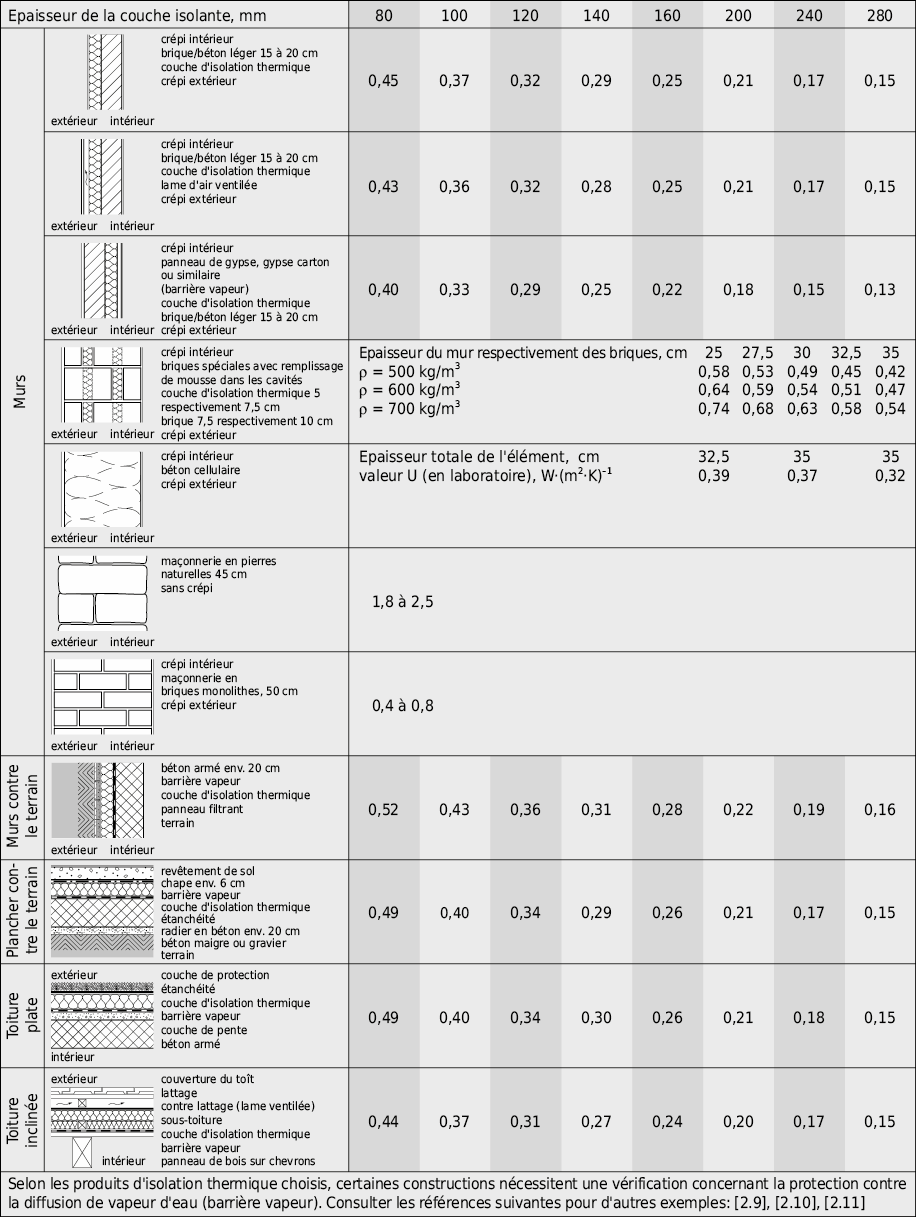
Valeur U: coefficient de transmission thermique
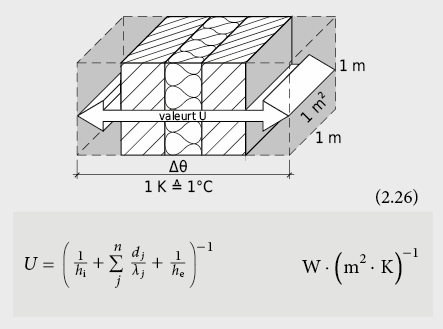
Le coefficient de transmission thermique U indique le flux de chaleur qui s’écoule, à l’état stationnaire, à travers une section de 1 m2 d’un élément de construction, perpendiculairement à sa surface et lorsqu’une différence de température de 1 K est maintenue entre ses deux faces.
Le pouvoir isolant d’une construction est d’autant meilleur que son coefficient de transmission thermique U est petit.
Les exigences d’isolation pour les murs et les toits peuvent, du point de vue actuel, être qualifées grossièrement de la manière suivante:

Quand la valeur U est connue, la densité du flux de chaleur q traversant un élément de construction soumis à une différence de température stationnaire Δθ = θi – θe se calcule par:

Dans les anciennes normes le coefficient de transmission thermique est désigné par k et le coefficient de transfert thermique surfacique par α.
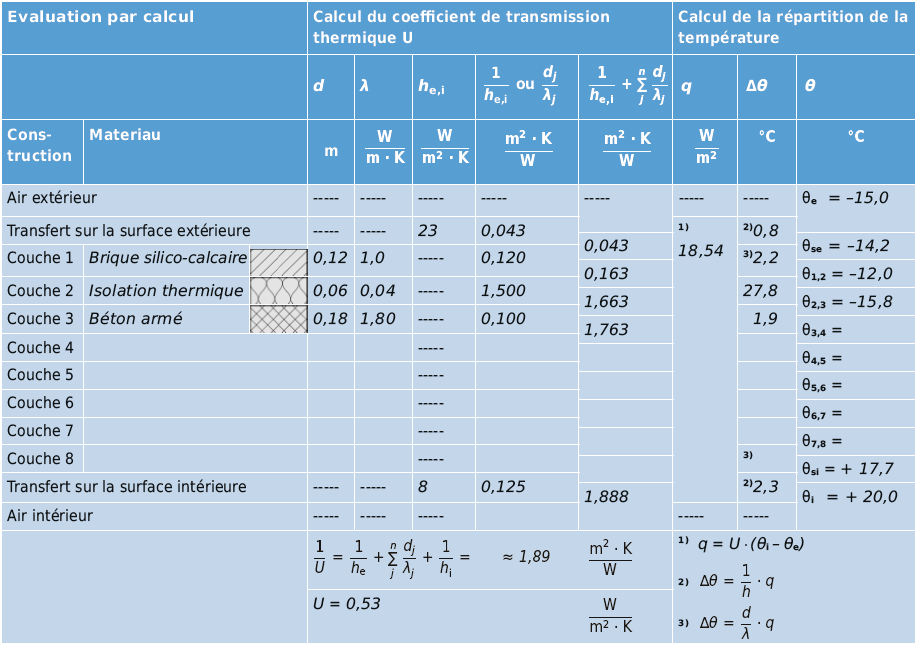
Détermination de la répartition de la température dans un élément de construction
a) par calcul
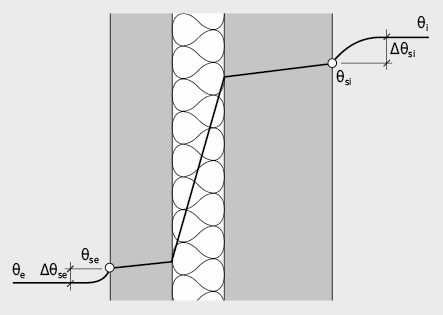
Aux surfaces on observe les écarts de température suivants:

Ecart de température sur la couche j:

Ecart de température à la profondeur x (depuis l’extérieur):
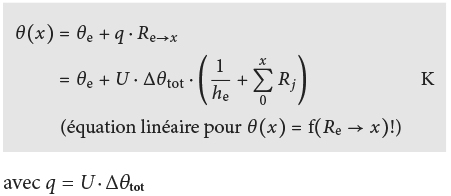
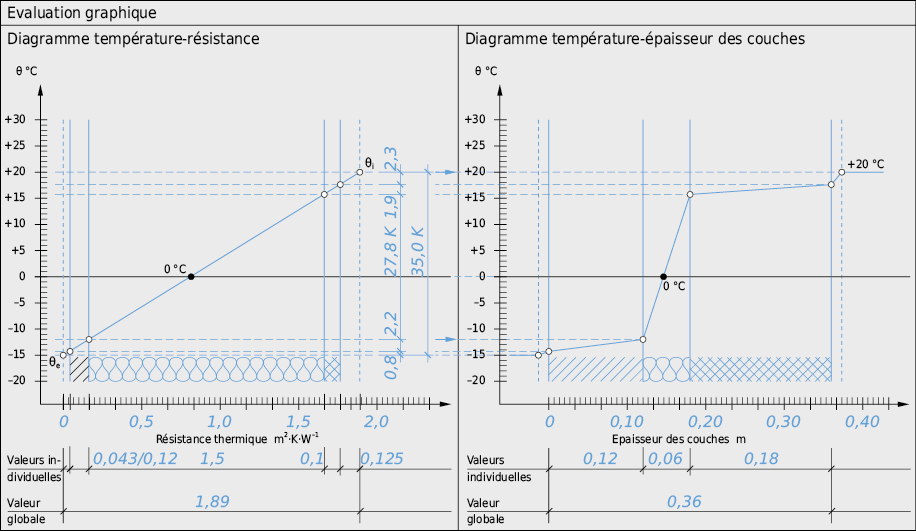
b) graphiquement
La dernière équation pour le calcul de la répartition de la température représente une droite de pente q = U · (θi – θe) quand on reporte sur l’axe x les résistances thermiques correpondant à chaque couche (1/hi, dj/λj, 1/he). On obtient la répartition de la température dans l’élément graphiquement de la manière suivante (voir Fig. 2.18):
- Une droite est tirée dans le diagramme Température-Résistance sur la base de la résistance thermique 1/U et des deux températures d’air θi und θe. Les températures aux interfaces entre les couches ou dans chaque couche peuvent se lire en fonction de leurs résistances thermiques.
- Les températures à chaque interface entre couches tirées de 1. sont reportées dans le diagramme Température-Epaisseur des couches en fonction de la profondeur des interfaces (→transformation de l’axe x tout en conservant la graduation de l’axe y). A l’intérieur de chaque couche de matériau, la répartition de la température est linéaire.
Résistances thermiques et …
Par analogie entre transport de charges électriques et transport de chaleur avec

on peut convertir la résistance électrique
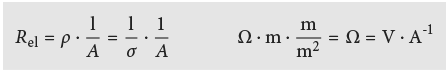
en résistance thermique
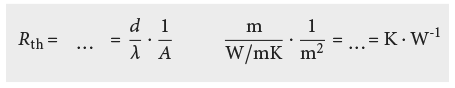
Dans les normes « thermiques » applicables, on se réfère aux valeurs U des éléments de construction ce qui a conduit à ne plus employer le terme de « résistance » comme relation entre une cause (Δθ) et son effet résultant (Фth). Ainsi on remarquera que c’est bien l’inverse de la valeur U qui décrit la résistance thermique spécifique d’un élément de construction.
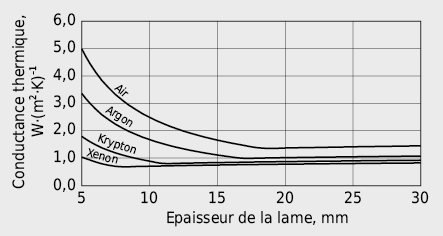
Valeur U des vitrages
Le transfert thermique à travers l’espace entre deux verres d’un vitrage se produit par rayonnement, convection et conduction (voir les bases du calcul à la section 2.1.4). Les propriétés de convection et conduction peuvent être réduites par l’emploi de gaz rares tels que l’Argon, le Krypton et le Xénon. Pour chacun de ces gaz, il existe une largeur optimale pour laquelle la conductance thermique par convection/conduction présente un minimum (voir Fig. 2.20). Cette largeur est de 8 mm pour le Xénon, 12 mm pour le Krypton, 16 mm pour l’Argon et 18 mm pour l’air.
Le transfert de chaleur par rayonnement peut être réduit en utilisant des revêtements de couleur neutre et réféchissants dans le domaine infrarouge. L’effet de ce genre de revêtement sur la conductance thermique par rayonnement est caractérisée par l’émissivité ε: plus petite est l’émissivité, plus cette conductance sera réduite.
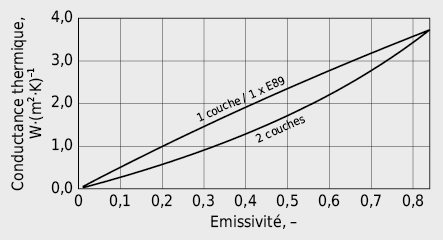
Dans la pratique, des revêtements sont disponibles avec les émissivités suivantes:
- Revêtements pyrolytiques ε = 14–20 % (E16)
- Revêtements par dépôt de vapeur ε = 8–12 % (E10)
- Revêtements par dépôt de vapeur ε = 4–6 % (E5)
- Revêtements par dépôt de vapeur ε = 2–4 % (E3)
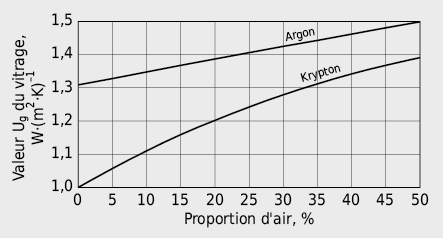
Avec des gaz rares, le taux de remplissage et le taux de fuite doivent être considérés. La valeur U d’un vitrage isolant double est illustrée à la figure 2.22 en fonction de la proportion d’air présente dans le remplissage de gaz rare.
Le tableau 2.11 donne un aperçu des vitrages isolants (VI) disponibles sur le marché avec leurs propriétés thermiques et optiques.
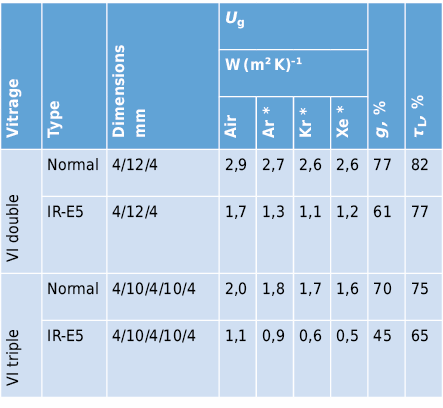
Valeurs U des fenêtres
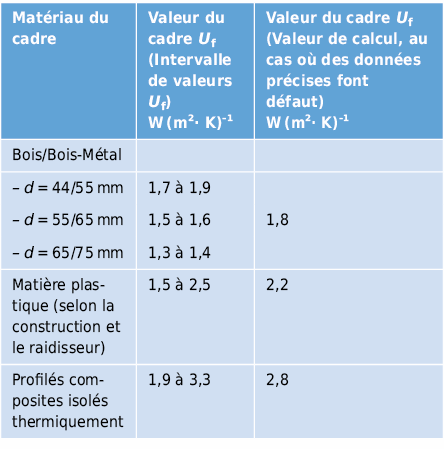
Le vitrage, les cadres de fenêtres ainsi que l’intercalaire ont des propriétés d’isolation thermiques différentes. Ainsi, pour déterminer la valeur UW d’une fenêtre, les éléments suivants doivent être distingués (voir [2.7] et [2.14]):
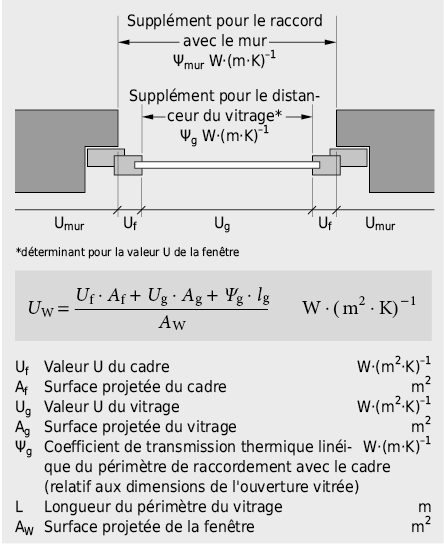
Des données détaillées concernant les valeurs U de vitrages et de fenêtres sont rassemblées dans l’annexe 9.12.
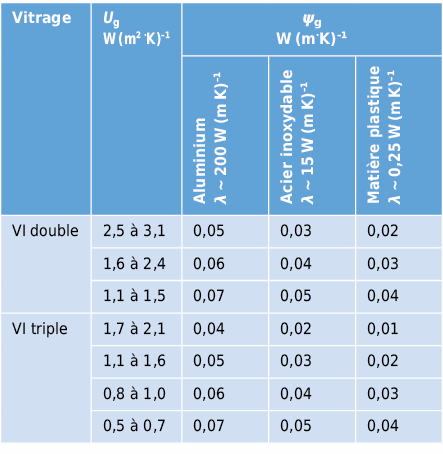
(Uf ≈ (1.5–2) W/(m2·K), définition de Ψg voir section 2.3.4)
2.1.6 Echanges de rayonnement avec l’environnement
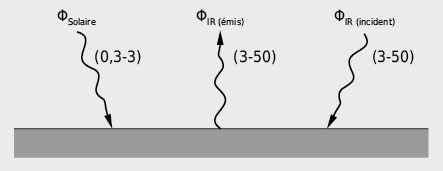
Les phénomènes suivants participent aux échanges de rayonnement entre l’enveloppe d’un bâtiment et son environnement:
- l’irradiance solaire de courte longueur d’onde, ΦSolaire
- l’émission de rayonnement de grande longueur d’onde (infrarouge) des surfaces, ΦIR(émis)
- l’irradiance à grande longueur d’onde (infrarouge) de l’environnement (atmosphère et terrain), ΦIR(incident)
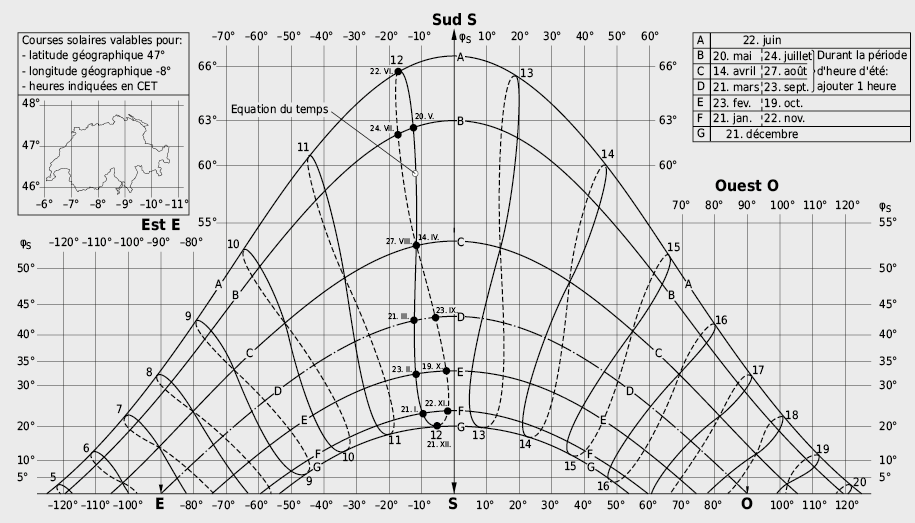
Pour déterminer l’irradiance solaire incidente sur la surface d’un élément de construction, la position du soleil par rapport à la normale à la surface éclairée doit être connue. Dans le cas de l’irradiance solaire directe on a:



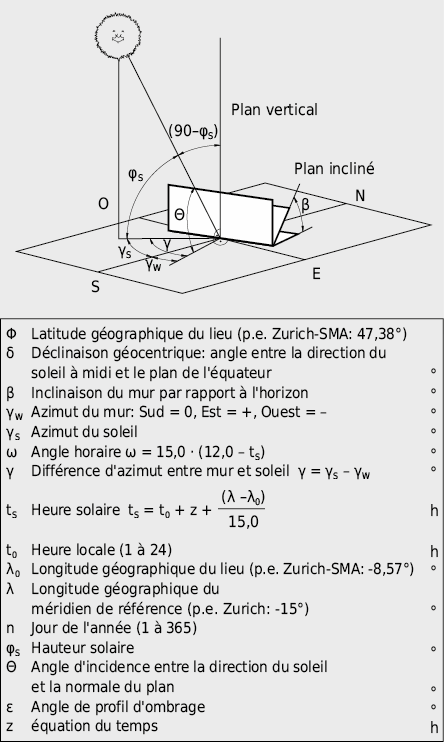
Le cycle annuel du soleil peut être déterminé simplement à l’aide du diagramme de la course solaire de la Fig. 2.28.

Pour obtenir l’irradiance solaire globale IG sur une surface inclinée, on doit, en plus de l’irradiance directe IB, également tenir compte de l’apport diffus du ciel (nuages éventuels inclus) et des réflexions diffuses sur le terrain:
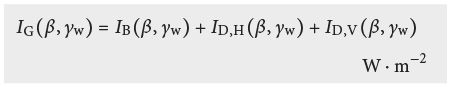
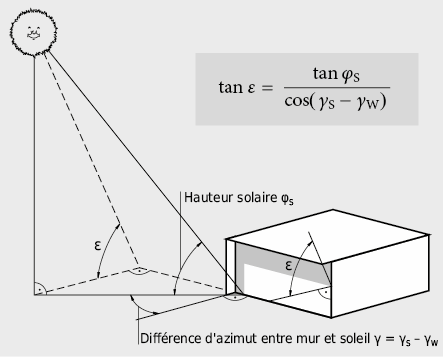
En présence d’obstructions, la zone ombrée peut être déterminée comme suit:
Lorsque l’irradiance globale ainsi que l’irradiance diffuse sur une surface horizontale sont spécifiées en fonction de la hauteur du soleil φS, l’irradiance globale pour un instant donné peut être estimée comme suit (modèle à trois composantes de rayonnement [2.24]):

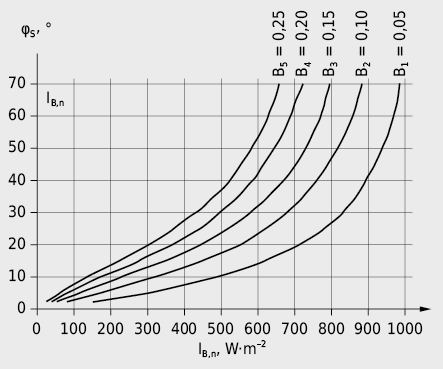
Dans le cas d’un mur vertical, l’irradiance diffuse ID,W peut être évaluée à l’aide des diagrammes de la Fig. 2.29:
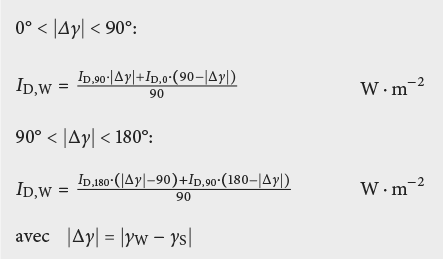
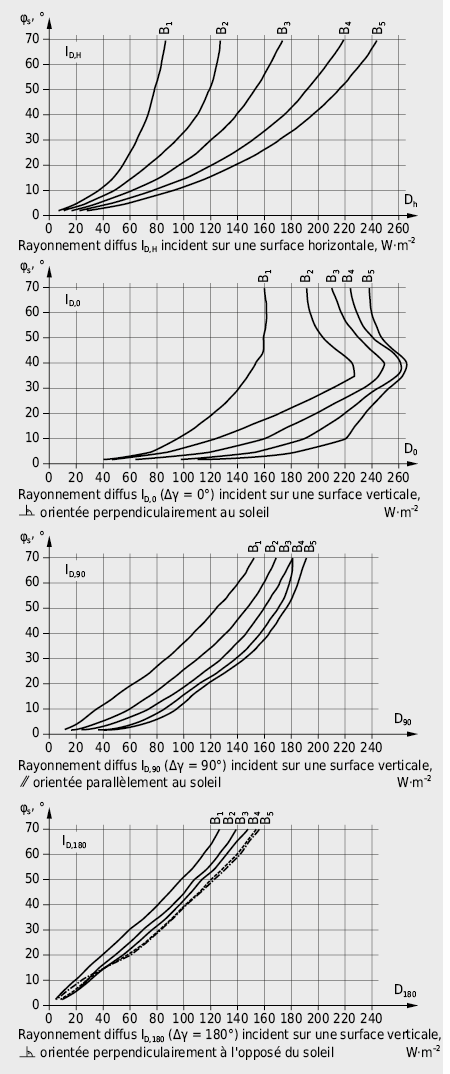
B2 = 0,10: air en milieu rural par beau temps en été
B3 = 0,15: air en milieu urbain par beau temps en été
B4 = 0,20: air avec brume épaisse
B5 = 0,25: air très brumeux par temps estival chaud et humide
L’irradiance diffuse sur une surface inclinée peut être obtenue d’une manière analogue en interpolant les valeurs obtenues pour une surface horizontale et la surface verticale correspondante (voir Fig. 2.29).
Pour plus de détails concernant la génération de valeurs horaires pour le rayonnement solaire local, on se référera au logiciel METEONORM et à sa documentation [2.24].
Dans le domaine infrarouge, l’irradiance provenant de l’environnement (atmosphère et site) s’oppose au rayonnement thermique émis par une surface. La déperdition thermique résultante peut être décomposée en deux parts:
- une déperdition thermique vers le voisinage (ε ≈ 1) qui se trouve au niveau de la température extérieure. Cette part est généralement considérée au travers du coefficient de transfert thermique hr, env inclus avec le coefficient de transfert surfacique par convection dans le coefficient de transfert surfacique he.
- un supplément de pertes dans le domaine infrarouge dû au déficit de rayonnement par ciel clair (voir Fig. 2.7). Ce supplément de pertes infrarouges ΔIR peut être estimé numériquement comme suit [2.16]:

L’émissivité du ciel clair dépend en premier lieu de la température du point de rosée de l’air extérieur. La corrélation suivante selon [2.15], [2.16] peut être utilisée:

Par ciel couvert, l’émissivité selon Unsworth [2.17] peut être estimée comme suit:

Eléments opaques
L’influence des composantes rayonnantes de courtes et grandes longueurs d’onde sur la transmission thermique peut être décrite à l’aide de ce que l’on dénomme la température rayonnante de l’air θe*. On entend, sous ce terme, une température d’air extérieur fictive (« corrigée ») conduisant à une densité de flux thermique, à travers l’élément de construction, identique à celle enregistrée lorsqu’il est soumis à l’influence du rayonnement (voir [2.19]).

Eléments transparents
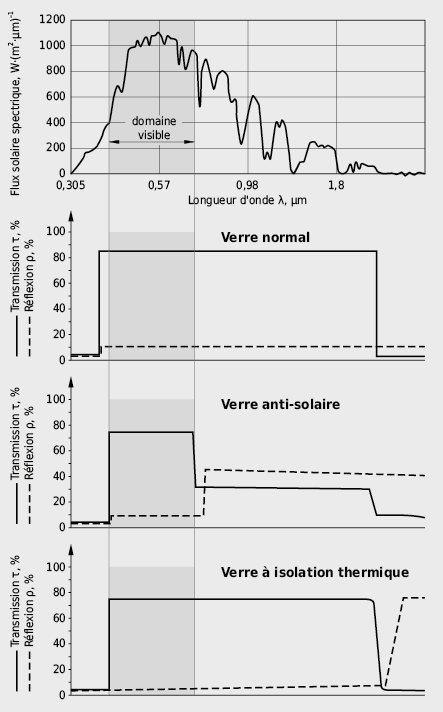
A travers les éléments transparents, une partie du rayonnement solaire parvient à l’intérieur du bâtiment tandis qu’une part est réfléchie par les vitrages et qu’une autre part est absorbée par les couches (de verre principalement) (voir Fig. 2.30). Le taux de transmission d’énergie globale g d’un vitrage indique quelle part du rayonnement extérieur incident aboutit sous forme de chaleur à l’intérieur du bâtiment. Pour déterminer les grandeurs caractéristiques selon EN 410 [2.13], les données spectrales des vitrages utilisés sont indispensables (voir Fig. 2.31).
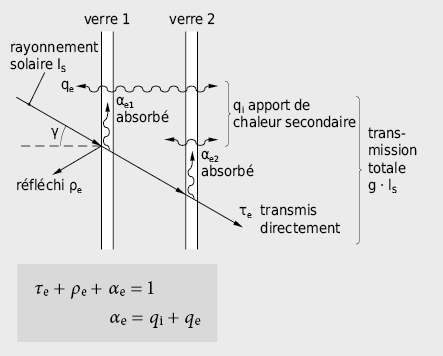

L’apport de chaleur secondaire vers l’intérieur peut se calculer de la façon suivante:
Vitrage simple:

Vitrage double:
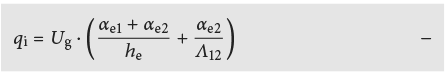
Vitrage triple:

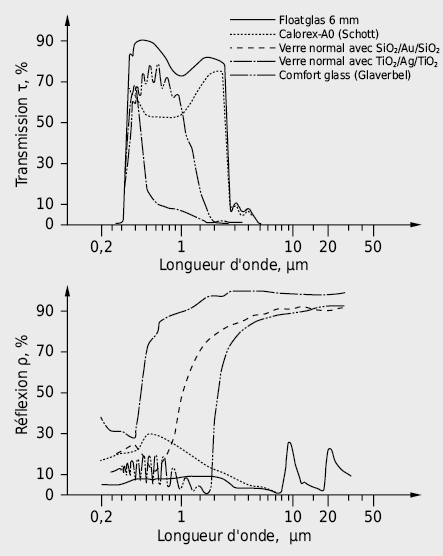
Les propriétés de transmission et de réflexion des vitrages peuvent être modifiées, selon leur fonction, par des revêtements métalliques. On distingue les produits suivants (voir aussi Fig. 2.32):
- Vitrages isolants
Réduction de la transmission de chaleur et haute transparence au rayonnement solaire et à la lumière visible
- Vitrages de contrôle solaire
Réduction de la transmisison du rayonnement solaire et haute transparence à la lumière visible
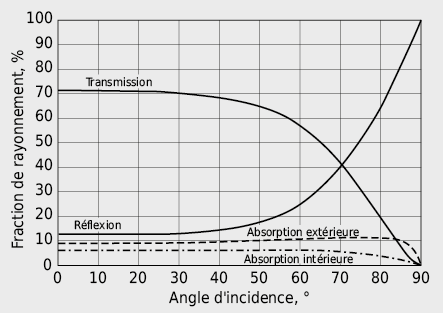
La figure 2.33 illustre l’effet de l’angle d’incidence sur le rayonnement parvenant sur un élément transparent.
Le bilan des flux de chaleur par m2 de vitrage peut être déterminé à l’aide de la formule suivante:
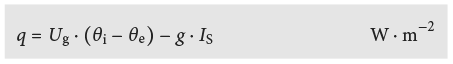
Lorsque les apports solaires deviennent importants, il faut prendre en compte que, suite à une élévation de la température à l’intérieur de la pièce, une part des apports ne peut pas être considérée comme thermiquement profitable (voir section 6.2.1, apports de chaleur utiles Qug). Dans le bilan énergétique la fenêtre doit, par conséquent, toujours être considérée avec l’intégralité du local. Les facteurs suivants influencent positivement l’utilisation de la chaleur provenant du rayonnement solaire:
- la masse d’accumulation thermique du local pour l’absorbtion de la chaleur excédentaire
- un réglage thermostatique par pièce ou une installation de chauffage à basse température pour l’adaptation immédiate de la puissance de chauffage aux besoins
Dispositifs de protection solaire
Les dispositifs de protection solaire tels qu’auvents, volets, stores ou stores à lamelles ont un effet sur la transmission du rayonnement solaire et de la lumière visible qui peut être déterminé, en combinaison avec le vitrage, par une procédure simplifiée selon EN 13363-1 [2.36]. La détermination du taux de transmission d’énergie globale gtot pour le rayonnement solaire et du facteur de transmission lumineuse τv,tot dépend de la position du système de protection solaire par rapport au vitrage et de l’état de la partie aveugle (fermée, disposition à 45° ou partie ouverte fixée). Pour le calcul, les paramètres caractéristiques du vitrage et du dispositif de protection solaire sont indispensables.
L’annexe 9.14 présente les exigences de protection solaire selon SIA 382/1 [2.39] ainsi que la procédure simplifiée selon EN 13363-1 [2.36] pour la détermination de la valeur g de vitrages en combinaison avec des systèmes de protection solaire.