Avec la contrainte d’économie d’énergie, pas uniquement dans le domaine du chauffage mais aussi pour l’éclairage, une utilisation optimale de la lumière naturelle s’impose.
Le rayonnement solaire global, d’une part gratuit et d’autre part plus ou moins disponible tout au long de la journée selon le temps, est perçu par l’œil humain dans le domaine spectral allant de 0,38 µm à 0,78 µm (→ Lumière naturelle).
-
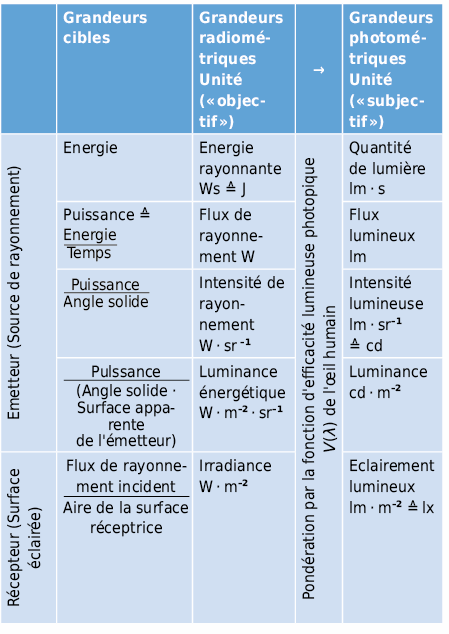
Quantité de lumière émise par une source lumineuse par unité de temps (correspond à une puissance en Watt).
-
Quantité de lumière rayonnée dans l’angle solide Ω (Ω = A/r2 ; A: Surface d’une sphère, r : Rayon de la sphère, angle solide total Ω = 4 π).
-
Quantité de flux lumineux incident sur une surface AE (surface apparente). L’éclairement décroît avec le carré de la distance r (Ev = Iv/r 2).
-
Impression visuelle de clarté procurée par un objet lumineux dont la surface AL · cos φ1 est perçue par l’œil (surface rayonnante apparente du point de vue de l’observateur) ou par une surface éclairée A possédant un facteur de réflexion ρ* (source secondaire d’éclairage).
La photométrie s’occupe de la mesure du rayonnement visible. Dans ce cadre les grandeurs purement physiques ne sont pas les seules à être intéressantes mais aussi l’impression sensorielle de la lumière. Pour cette raison on définit, tout en respectant les lois de l’optique géométrique, ce que l’on appelle des grandeurs physiologiques, soit pour l’entier du domaine spectral visible, soit pour une longueur d’onde ou une plage de longueurs d’onde déterminée.
La relation entre grandeurs physiologiques et physiques est compliquée car l’œil présente une sensibilité qui varie avec la fréquence et l’intensité. Par conséquent, les unités photométriques physiologiques ont été incorporées en supplément dans le système international d’unités.
5.1.1 Evaluation du rayonnement
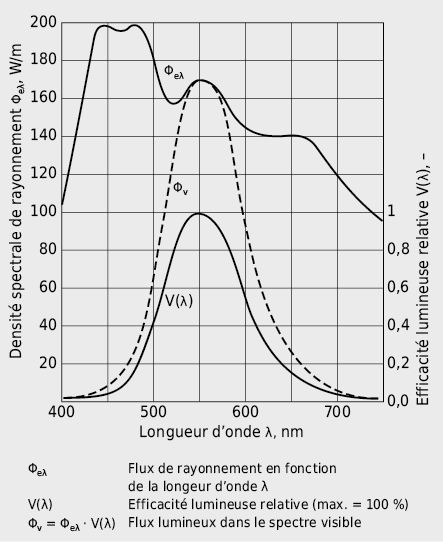
L’impression de clarté ne dépend pas uniquement de la puissance du rayonnement (en W) capté par l’œil mais aussi de la répartition spectrale de ce rayonnement.
Les différents stimuli lumineux monochromatiques génèrent des sensations lumineuses différentes en fonction de leurs longueurs d’onde. Par exemple, pour une même puissance, un stimulus lumineux monochromatique à 550 nm de longueur d’onde est perçu comme beaucoup plus clair que des stimuli lumineux à 400 nm ou 700 nm de longueurs d’onde.
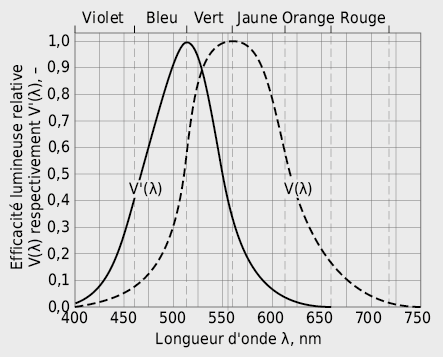
Ces deux fonctions de pondération (voir Fig. 5.2) définissent l’observateur de référence photométrique selon la CIE [5.1] pour la vision diurne respectivement nocturne.
La fonction CIE V(λ) est valable pour la vision diurne. On parle de la vision de jour (vision photopique, vision par les cônes), quand la luminosité est suffisamment élevée pour que les couleurs soient clairement reconnaissables.
-
V(λ) Œil adapté à la lumière (vision diurne)
-
V '(λ) Œil adapté à la pénombre (vision nocturne)
Pour la vision nocturne, c.à.d. quand la luminosité devient si faible que les couleurs ne peuvent plus être reconnues, c’est la fonction CIE V ’(λ) qui est appliquée.
Les instruments de mesures photométriques, en particulier le luxmètre, sont presque sans exception ajustés et calibrés pour la vision de jour. De même, toutes les grandeurs employées en technique de l’éclairage se basent sur la fonction V(λ).
A partir du flux de rayonnement Φe , dont la répartition dans le spectre est spécifiée par le flux spectral de rayonnement Φeλ(λ), le flux lumineux par vision de jour Φv s’obtient par la pondération photométrique (voir Fig. 5.3) à l’aide de l’équation:
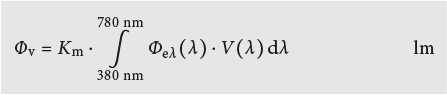
Le flux lumineux par vision nocturne Φv‘ s’obtient par l’équation:
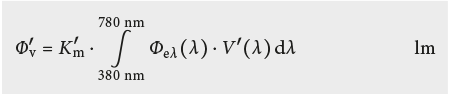
Les constantes Km et K ’m sont les efficacités lumineuses maximales par vision diurne et respectivement nocturne:

5.1.2 Flux lumineux et intensité lumineuse
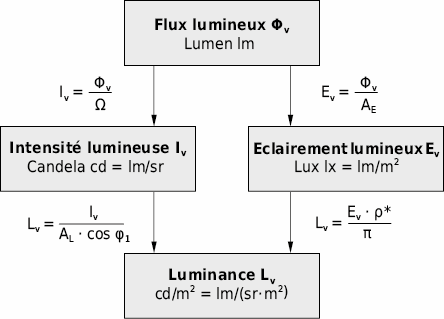
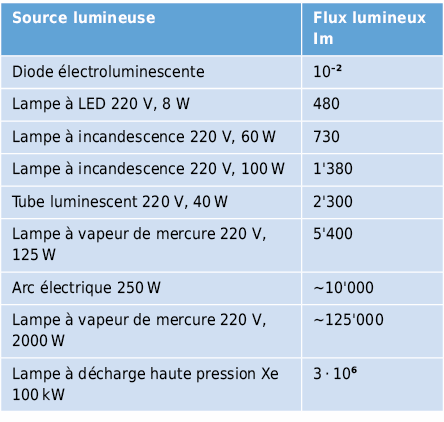
La totalité du flux de rayonnement émis par une source lumineuse et pondéré par la sensibilité de l’œil s’appelle flux lumineux. L’unité physiologique du flux lumineux Φv est le Lumen (lm).
La surface plane A1 d’une source lumineuse émet sous l’angle φ1 par rapport à sa normale un flux lumineux Φv dans un petit angle solide Ω (voir Fig. 5.4):
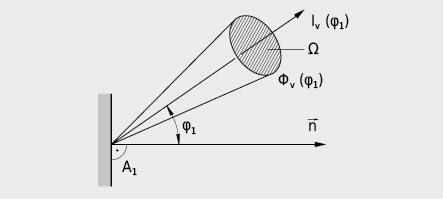

ou encore:

Iv (φ1) représente l’intensité lumineuse. L’unité physiologique Candela (cd) de l’intensité lumineuse Iv est aussi une unité de base du système international d’unités SI. Le flux lumineux total Φv, tot se calcule par:

5.1.3 Luminance
Comme les sources lumineuses ont des formes étendues et émettent leurs rayonnements depuis la totalité de leurs surfaces, on décrit leurs propriétés à l’aide de la grandeur supplémentaire dénommée luminance Lv , qui représente le rapport entre l’intensité lumineuse Iv (φ = 0) et la surface de l’élément lumineux:

La même définition est aussi valable par analogie pour une surface éclairée mais n’émettant pas de rayonnement propre.
Quand la surface lumineuse est observée sous un angle φ1, la relation générale suivante s’applique:

La luminance dépend des propriétés de la surface notamment du matériau, de l’état de surface et de la température. Plusieurs matériaux ayant des surfaces réfléchissantes rugeuses, comme par exemple le plâtre ou le carton, apparaissent avec la même luminosité dans toutes les directions. Quand on les observe de côté, l’intensité lumineuse diminue avec le cosinus de l’angle d’émission alors que la surface apparaît aussi comme réduite du même facteur. Il s’ensuit que la surface apparaît toujours aussi lumineuse à l’œil. Ce type de surfaces ou de sources lumineuses présentant des luminances indépendantes de la direction est appelé émetteur Lambert.
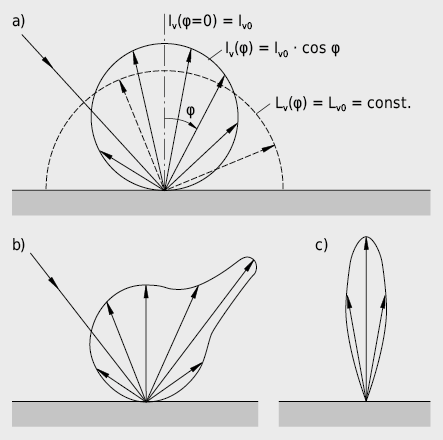
a) réflexion diffuse (loi de Lambert)
b) papier blanc (angle de brillance!); en comparaison:
c) caractéristique d’émission d’une diode électroluminescente
Comme la lune et le soleil brillent uniformément sur la totalité de leurs surfaces, on les considère dès lors aussi comme des émetteurs Lambert.
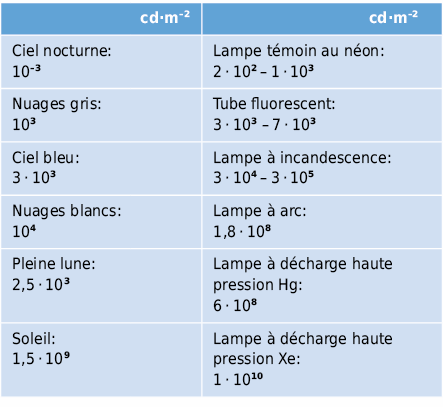
5.1.4 Eclairement lumineux
La reconnaissance des détails d’un objet dépend, entre autres, de la quantité de flux lumineux parvenant à sa surface que l’on dénomme l’éclairement lumineux Ev .

Une surface reçoit un éclairement lumineux Ev de 1 Lux (lx) lorsqu’un flux lumineux de 1 lm lui parvient perpendiculairement et uniformément sur une aire de 1 m2. (Attention: AE représente la surface réceptrice apparente, perpendiculaire au flux incident!)
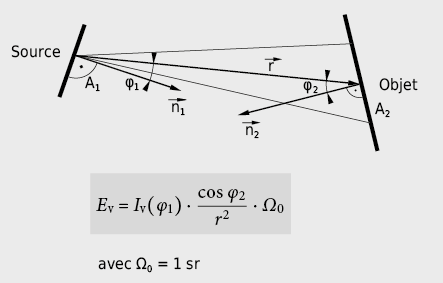
L’éclairement lumineux est indifférent à la direction d’où provient la lumière incidente sur l’élément de surface. Cependant, l’éclairement lumineux incident sur une surface plane dépend de la position de celle-ci dans le faisceau lumineux qui l’éclaire.
Les exigences sur l’éclairement lumineux dépendent des activités et sont spécifiées dans [5.9].
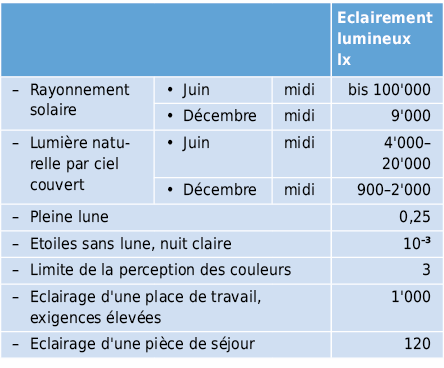
5.1.5 Comparaison entre grandeurs physiques et photométriques caractérisant le rayonnement