9.1.1 Physique, physique du bâtiment et vision intégrale
La physique du bâtiment en tant que physique appliquée à la construction ainsi que le « background » constitué des bases physiques correspondantes forment une base indispensable pour une activité soutenable des architectes ainsi que des ingénieurs en construction et technique du bâtiment. D’une part, la complexité des tâches acuelles à acccomplir demande toujours plus de connaissances spécialisées, d’autre part les solutions optimales nécessitent une réflexion interdisciplinaire et un travail d’équipe entre les partenaires qui participent à un projet. Cependant, la physique en tant que «langage spécialisé» commun est parfois difficilement compréhensible. C’est pourquoi la suite de ce chapitre tente de présenter à l’aide d’analogies la façon de penser de la physique et son utilisation.
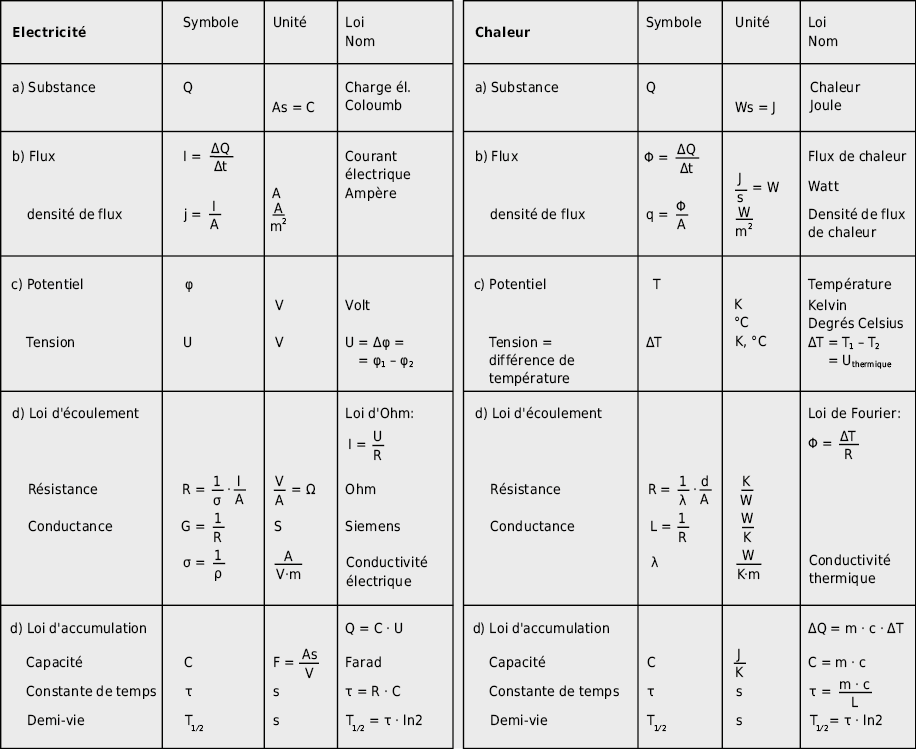
Plusieurs processus peuvent être analysés à partir des mêmes principes de base et sont ramenés à des «formalismes» similaires. Les relations entre différentes branches de la physique apparaissent sous des formes mathématiques analogues. Dès lors, il est intéressant d’analyser les phénomènes physiques importants pour le bâtiment à l’aide d’observations par analogies selon des points de vues «homogènes» (voir Fig. 9.1.2).
Comme une délimitation claires des systèmes est indispenable pour l’établissement de bilans, ce qui cause le «moins» de difficultés pour les circuits électriques, les principes de base et de travail de la physique se laissent le mieux décrire par de simples circuits électriques qui peuvent ensuite être appliqués de manière pertinente à d’importants domaines de la physique du bâtiment tels que:
- transport et accumulation de chaleur
- transport et accumulation de vapeur
- circulation de l’air
- circulation de l’eau
- propagation et accumulation du bruit
L’application technique au bâtiment doit cependant toujours demeurer au premier plan. Ceci exige parfois une simplification de la théorie au profit d’une application convenant à la pratique.
9.1.2 Principes généraux
- Grandeur conservée Il existe une grandeur quantifiable qui peut être comptée et mesurée. Si une partie disparaît d’un lieu, alors la même quantité doit réapparaître dans un autre lieu.
- Courant et densité de courant (effet) La variation temporelle d’une grandeur conservée se dénomme courant (I ou Φ). Un courant rapporté à une unité de surface est appelé densité de courant ou intensité.
- Potentiel et tension (cause)Pour qu’un courant s’écoule, une cause est indispensable. La cause est décrite comme une tension (U) ou une différence de potentiel (U = Δφ).
- Loi de courant ou loi de cause à effetDes résistances (R) s’opposent aux courants déclenchés par les tensions. La loi de courant décrit la relation entre la tension et le courant qui est dans de nombreux cas linéaire. L’inverse de la résistance se dénomme conductance. Le courant s’écoule toujours du potentiel le plus élevé vers le potentiel le plus faible. Si deux points possèdent le même potentiel, alors aucun courant ne circule entre eux.
- Equation d’accumulationSi une grandeur conservée s’écoule dans un accumulateur sans fuite, alors ce dernier se charge avec une tension croissante. Le facteur de proportionnalité se dénomme capacité (C). Dans la pratique, on s’intéresse aux charges/décharges d’accumulateurs qui suivent très souvent des lois exponentielles. Les valeurs caractéristiques d’un accumulateur sont la constante de temps (τ) et la demi-vie (Τ1 ⁄ 2).
9.1.3 Grandeurs physiques, unités de mesure
Pour formuler des relations et des lois, la physique emploie des équations mathématiques qui relient entre elles des grandeurs physiques. Les grandeurs physiques doivent être mesurables. Ainsi elles sont composées d’une déclaration quantitative {G} (valeur numérique) et d’une déclaration qualitative [G] (unité):
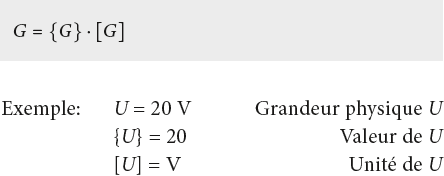
Pour comparer des grandeurs mesurables des unités de mesure sont nécessaires. Toutes les unités peuvent être déduites de ce que l’on dénomme les unités SI définies par l’Organisation internationale de normalisation (ISO) (voir annexe 9.4):
- Longueur m (mètre)
- Temps s (seconde)
- Masse kg (kilogramme)
- Quantité de matière mol (mole)
- Température K (kelvin)
- Courant électrique A (ampère)
- Intensité lumineuse cd (candela)
Equation de grandeurs:
- avec des termes: Energie = Puissance · Temps
- avec des symboles: E = P · t
Equation aux dimensions correspondante:
1 Ws (Wattseconde) = Watt · seconde = 1 W · 1s = 1 J (Joule)
Les unités physiques peuvent être manipulées comme des facteurs habituels; c’est-à-dire on peut par exemple les factoriser ou les simplifier. Ceci permet, en posant une équation aux dimensions, de faire un premier test d’exactitude formelle d’une équation aux grandeurs.
9.1.4 Equations phénomènologiques et équations d’état
Elles décrivent d’une part les relations entre des grandeurs physiques et des propriétés des matériaux et, d’autre part, relient des variables d’état (grandeurs qui ne dépendent que de l’état de départ et de l’état final). Par exemple:
- résistance ohmique d’un fil (Rel = ρ · l/A)
- équation générale des gaz (p · V = n · R · T).
9.1.5 Les règles des circuits
a) Circuit en série
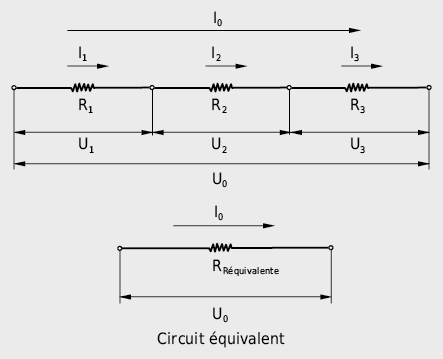
I0 = I1 = I2 = I3 = … = In : loi des noeuds
Ij = Uj / Rj = Uj · Gj : loi de courant
Le courant continu s’écoule sans ramification à travers une succesion de plusieurs résistances. C’est une conséquence de l’équation de continuité. La tension totale correspond à la somme des tensions partielles autour des résistances. Les tensions et les résistances sont proportionnelles entre elles.
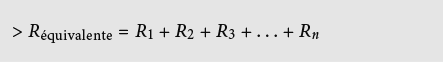
b) Circuit en parallèle
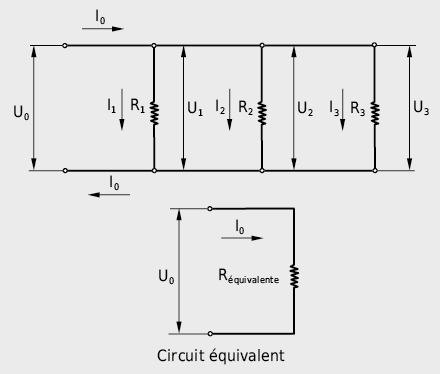
I0 = I1 + I2 + I3 + … + In : loi des noeuds
Ij = Uj / Rj = Uj · Gj : loi de courant
Plusieurs résistances connectées les unes à côté des autres sont soumises à la même tension. Le courant se répartit au noeud, de façon à ce que le courant total corresponde à la somme des courants partiels. C’est une conséquence du principe de conservation. Les courants se comportent comme la conductance. (PS : pour les fluides compressibles comme l’air, le principe de conservation n’est valable que pour le flux massique et pas pour le flux volumique).
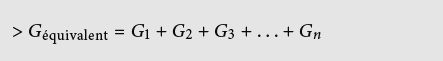
De façon analogue aux circuits purement résistifs, des règles correpondantes peuvent être posées pour des accumulateurs de charges ou capacités. Les principes sont identiques; comme une capacité a un fonctionnement différent de celui d’une résistance, la « loi fonctionnelle » de l’élément doit être remplacée par la loi d’accumulation:
- capacités placées en série:
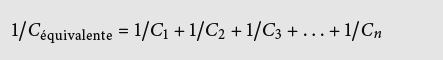
- capacités placées en parallèle:
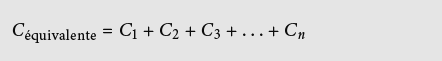
Les principes de base, les gradeurs physiques et les unités de mesures, les équations phénomènologiques et les équations d’état forment, ensemble avec les règles des circuits, un premier instrumentarium simple pour la résolution de problèmes physiques.
Souvent, les difficultés principales ne se trouvent pas dans la physique elle-même mais résident plutôt dans l’établissement clair des limites du système et des conditions aux bords, dans la récolte de données fiables ainsi que dans une modélisation optimale.
9.1.6 Processus stationaires et instationaires
Dans la nature réelle et aussi dans le bâtiment la plupart des processus évoluent de manière instationnaire, c’est-à-dire que les variables d’entraînement qui sont à l’œuvre comme la pression atmsophérique, la température, l’humidité etc. de même que les propriétés des matériaux varient au cours du temps. Ces variations temporelles posent des difficultés dans la compréhension intellectuelle des relations de cause à effet et compliquent les évaluations par calculs.
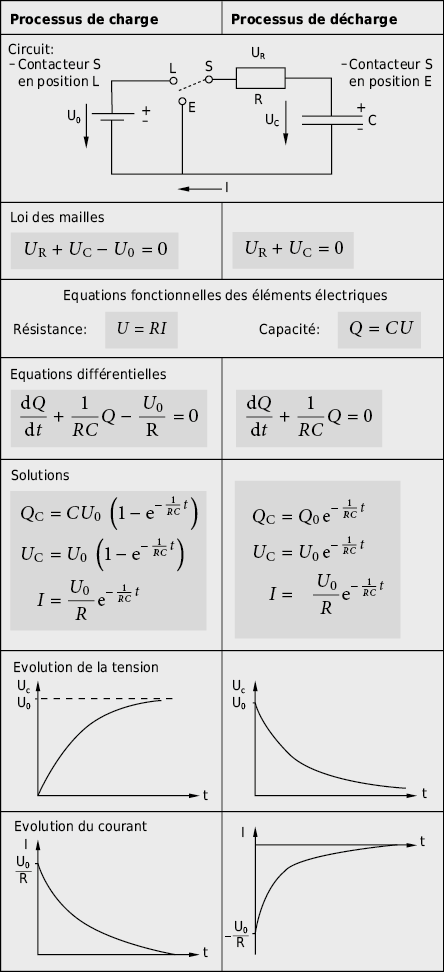
Comme dans de nombreux cas les variations évoluent lentement ou que leurs amplitudes sont faibles, on peut éventuellement renoncer au calcul instationnaire exact et calculer de manière stationnaire avec des paramètres d’utilisation moyens. Toutefois il existe des phénomènes dont le processus dépend tellement d’une évolution instationnaire qu’une approximation avec des conditions aux bords constantes n’est plus sensée. La charge ou décharge d’un accumulateur de chaleur est un exemple de processus instationnaire pour lequel un moyennage ne conduit à aucune conclusion raisonnable sur l’état de charge.
La diversité des processus instationnaires est si grande qu’un mode de traitement systématique n’est pas possible. En outre, dans de tels cas on ne parvient au but qu’avec des notions mathématiques pointues (équations différentielles) et/ou à l’aide de programmes informatiques. Cependant l’utilisation d’outils de calcul numérique ne constitue pas un visa permettant d’éviter toute réflexion et analyse critique. Les machines dépassent les humains uniquement pour la précision, la vitesse de calcul et la capacité de stockage; les résultats de calcul par odinateurs ne sont pas plus précis que les programmes et données qui les alimentent!
Le traitement stationnaire ou instationnaire d’un processus est d’une importance élevée et a une portée capitale. L’objectif attendu d’un calcul détermine la pertinence de l’une ou l’autre manière de voir. Si l’on s’intéresse par exemple aux déperditions moyennes par ventilation d’un bâtiment influencé par le vent, un calcul stationnaire sur un intervalle de temps suffisamment long peut être pertinent. Si la discussion porte sur la résistance d’un élément de construction ou même sur la sécurité d’un bâtiment entier, alors le comportement instationnaire du vent doit absolument être considéré puisque une rafale unique peut éventuellement causer un dégât. Des perturbations périodiques (par exemple la variation journalière de la température extérieure sur 24 h) et impulsionnelles (par exemple les processus d’enclenchement et de déclenchement du chauffage) sont des exemples de conditions aux bords instationnaires qui jouent un rôle central dans les bâtiments. Ici aussi des modèles électriques simples sont souvent employés par analogie pour l’étude et la résolution de problèmes concernant par exemple la thermique, l’hygiène de l’air ou l’acoustique des salles.
9.1.7 Physique – Physique du bâtiment – Pratique de la construction?
Comme les problèmes pratiques à résoudre actuellement ont souvent un fort caractère interdisciplinaire, l’utilisation appliquée de la physique en tant que science fondamentale et la collaboration avec d’autres disciplines jouent un rôle central. Il est d’une part indispensable de faire recours à des modèles physiques, des théories, des lois mais aussi à des méthodes de travail de la physique pour la compréhension des phénomènes et processus qui existent dans la nature et l’environnement construit. D’autre part, un «réel» problème pratique est, au début, le plus souvent difficilement résoluble physiquement et mathématiquement. Le problème doit premièrement être «idéalisé», c’est-à-dire qu’il faut le transformer pour le décrire quantitativement ou au moins qualitativement par des grandeurs physiques. Cette transformation s’appelle modélisation. Ce n’est que ce problème débarrasé de ses « détails insignifiants » qui peut alors être étudié par des méthodes physiques. Quand il est établi que le modèle et ses hypothèses sont reproductibles dans toutes les directions et qu’il est quantitativement vérifiable, généralement à l’aide de méthodes mathématiques, on parle alors d’une théorie. La solution du problème purement physique doit être vérifiée par des expériences/mesures, puis interprétée sous l’angle du problème «réel» et éventuellement complétée par des adaptations pratiques conformes à la réalité.
Cette méthode de travail, ce cycle
- observation/Analyse
- établissement d’un modèle
- théorie
- vérification
- correction/adaptation
est valable tant pour des phénomènes physiques « idéalisés » que pour de « réels » processus liés aux bâtiments.