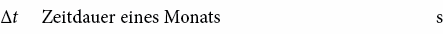6.4.1 Speicherverhalten des Gebäudes ⓘ
Aufwärmverhalten
Die Aufwärmung eines Gebäudes oder Raumes durch interne Wärmequellen wie Personen, Beleuchtung, Geräte und durch Sonneneinstrahlungsgewinne der Fenster ist vom Speichervermögen der Raumumschliessungsflächen abhängig. Als Beurteilungsgrösse für das Speichervermögen kann die speicherwirksame Masse Mj der Bauteile (vgl. Kap. 2.2) herangezogen werden. Die Raumspeichermasse m‚ kann wie folgt ermittelt werden:

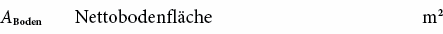
Die so berechnete flächenbezogene Masse m‚ des Raumes erlaubt eine Klassierung der Bauweise bezüglich des Wärmespeichervermögens (→ Bauschwereklassen [6.3]):

Auskühlverhalten
Das Auskühlen eines Gebäudes oder Raumes oder allgemein eines Speichers kann mit Hilfe einer Exponentialfunktion beschrieben werden (analog dem Entladen eines Kondensators, vgl. Kap. 9.1.6).
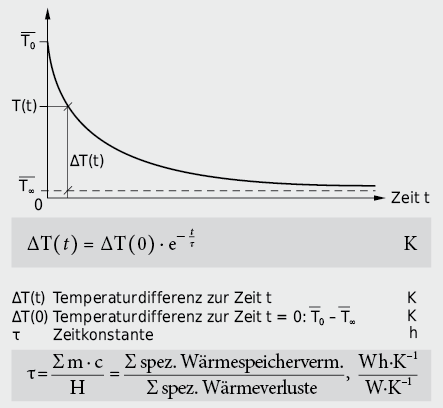
6.4.2 Speicherverhalten des Erdreiches und Wärmeverluste gegen Erdreich
Stoffwerte des Erdbodens
Die thermischen Eigenschaften des Erdbodens hängen von mehreren Faktoren ab, zu denen Dichte, Grad der Wassersättigung, Teilchengrösse, Art des die Teilchen bildenden Minerals, ob gefroren oder ungefroren, gehören. Deshalb ändern sich die thermischen Eigenschaften stark von Ort zu Ort und in unterschiedlichen Tiefen an einem gegebenen Ort, und sie können sich infolge Veränderung des Feuchtegehaltes oder infolge Vereisens und Tauens auch zeitlich ändern.
Werte der Eigenschaften des für die Wärmeverlustberechnungen verwendeten Erdbodens, einschliesslich Messwerte, sollten für den Erdboden in der Umgebung des Gebäudes und über den Zeitraum, auf den sich die Berechnung bezieht (z. B. die Heizperiode), repräsentativ sein.
Die folgende Tabelle gibt den Bereich der Wärmeleitfähigkeit für unterschiedliche, ungefrorene Erdböden an.
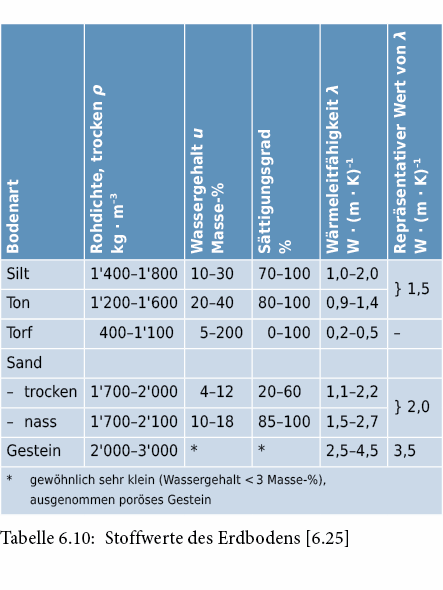
Die Wärmekapazität je Volumeneinheit kann wie folgt bestimmt werden:
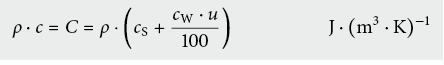

Für die meisten Materialien ist cS ≈ 1000 J · (kg · K)–1, und für Wasser ist cW ≈ 4180 J · (kg · K)–1 bei 10 °C. Für die in Tabelle 6.10 vorgestellten Erdmaterialien ergeben sich somit folgende, mittlere Wärmekapazitäten:
- Ton/Silt: C ≈ 3 · 106 in J · (m3 · K)–1
- Sand: C ≈ 2 · 106 in J · (m3 · K)–1
- Gestein: C ≈ 2 · 106 in J · (m3 · K)–1
Monatliche Wärmeverlustberechnung
Um die Wirkung der grossen Wärmeträgheit des Erdbodens zu berücksichtigen, wird die Wärmeübertragung durch eine stationäre oder mittlere Komponente zusammen mit der jährlichen periodischen Komponente dargestellt. Die stationäre Komponente ist auf die Differenz zwischen jährlicher mittlerer Innentemperatur und jährlicher mittlerer Aussentemperatur, die periodische Komponente auf die Amplitude der Schwankung der Innen- und Aussentemperatur um ihre entsprechenden Mittelwerte bezogen.
Für die Berechnung entsprechend EN ISO 13370 [6.25] wird angenommen, dass Innen- und Aussentemperatur in folgender Form sinusförmig um ihre jährlichen Mittelwerte schwanken:
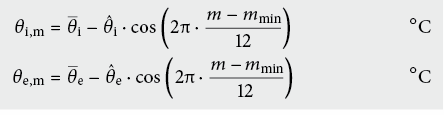

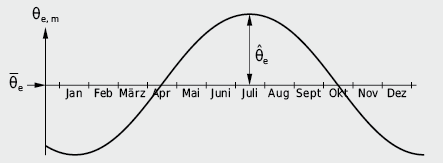
Die Definitionen von θ e und ![]() sind in Abbildung 6.10 dargestellt. Das gleiche gilt für die Innentemperaturen.
sind in Abbildung 6.10 dargestellt. Das gleiche gilt für die Innentemperaturen.
Anmerkungen:
- Auf der Nordhalbkugel kann mmin = 1 (Mindesttemperatur Mitte Januar) und auf der Südhalbkugel mmin = 7 (Mindesttemperatur Mitte Juli) angenommen werden.
- Für die Berechnungen sind nur die jährliche mittlere Temperatur und die jährliche Amplitude erforderlich: Diese Grössen können aus Monatswerten abgeleitet werden.
Der mittlere Wärmestrom im Monat m ist gegeben durch:
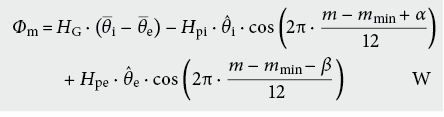

Anmerkungen:
- Die Gleichung setzt voraus, dass die jährliche Schwankung der Innentemperatur derart ist, dass
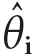 im Winter niedriger ist als im Sommer. Wenn das Umgekehrte gilt, sollte das Vorzeichen von
im Winter niedriger ist als im Sommer. Wenn das Umgekehrte gilt, sollte das Vorzeichen von 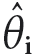 negativ gewählt werden.
negativ gewählt werden. - Für Berechnungen, die auf der Annahme einer konstanten Innentemperatur basieren, ist
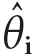 = 0, und Hpi braucht nicht betrachtet zu werden.
= 0, und Hpi braucht nicht betrachtet zu werden.
Wärmetransferkoeffizienten H
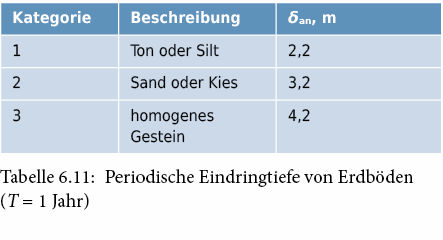
Die periodischen Wärmetransferkoeffizienten werden auf die periodische Eindringtiefe δ bezogen, d. h. auf die Tiefe im Erdboden, bei der (für eindimensionale Wärmeströmung) die Temperaturamplitude auf 1/e der Amplitude an der Oberfläche abgeklungen ist (siehe auch Abschnitt 2.2.1). Für einen jährlichen Temperaturzyklus ist δan gegeben durch:

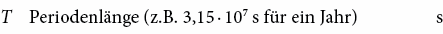
Richtwerte von δan sind in nachfolgender Tabelle zusammengestellt.
Der Wärmetransferkoeffizient infolge Schwankungen der Innentemperatur über einen jährlichen Zyklus besteht aus zwei Termen, einem Term, der sich auf die Kellerwände, und einem weiteren Term, der sich auf den Kellerfussboden bezieht:
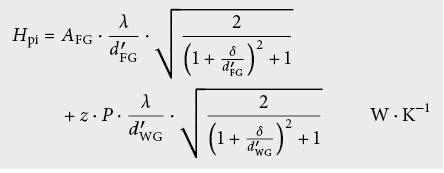
Der Wärmetransferkoeffizient infolge Schwankungen der Aussentemperatur über einen jährlichen Zyklus besteht aus zwei Termen, einem Term, der sich auf die Kellerwände, und einem weiteren Term, der sich auf den Kellerfussboden bezieht:
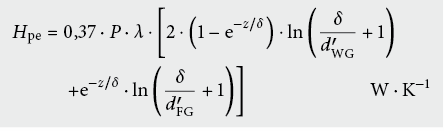

Der monatliche Wärmeverlust des Kellers ermittelt sich wie folgt: