9 Anhang

9.1.1 Physik, Bauphysik und integrale Denkweise

Bauphysik als angewandte Physik am Bau und die entsprechenden physikalischen Grundlagen als «Background» bilden eine unabdingbare Basis für eine nachhaltige Tätigkeit von Architekten, Bau- und Gebäudetechnikingenieuren. Die Komplexität der heute zu lösenden Aufgaben verlangt einerseits nach immer mehr Spezialwissen, andererseits erfordern optimale Lösungen interdisziplinäres Denken und Teamarbeit unter den beteiligten Projektpartnern. Die Physik als gemeinsame Sprache ist nun aber eine z. T. schwer verständliche, «spezielle Sprache», deshalb wird im Folgenden der Versuch unternommen, die Denkweise der Physik und das Arbeiten mit Analogien aufzuzeigen.

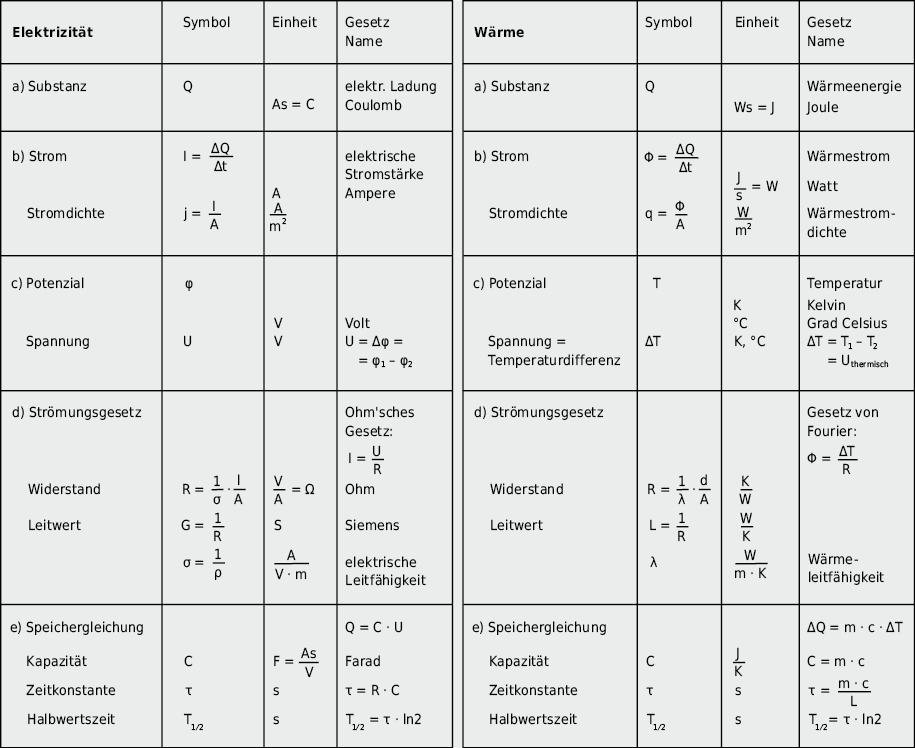
Viele Vorgänge können nach denselben Grundprinzipien analysiert werden und lassen sich auf ähnliche « Formalismen » zurückführen. Zusammenhänge aus unterschiedlichen Fachbereichen der Physik kommen in analoger mathematischer Form wieder vor. Daher ist es sinnvoll, wichtige physikalische Phänomene am Bau mit Hilfe von Analogiebetrachtungen nach «einheitlichen»  Gesichtspunkten zu analysieren (vgl. Abb. 9.1.2).

Da klare Systemabgrenzungen, die zum Erstellen von Bilanzen unerlässlich sind, bei elektrischen Netzwerken am «wenigsten» Schwierigkeiten bereiten, lassen sich die physikalischen Grund- bzw. Arbeitsprinzipien am ehesten an einfachen, erfassbaren Gleichstromkreisen entwickeln, um sie nachher sinngemäss auf wichtige Gebiete der Bauphysik, wie

• Wärmetransport und -speicherung
• Dampftransport und -speicherung
• Luftströmung
• Wasserströmung
• Schallausbreitung und -speicherung

übertragen zu können. Im Vordergrund hat dabei immer die ingenieurtechnische Anwendung am Bau zu stehen. Dies erfordert gelegentlich eine Vereinfachung der Theorie zugunsten einer praxistauglichen Anwendung.

9.1.2 Allgemeine Grundprinzipien

1. ErhaltungsgrösseEs existiert eine mengenartige Grösse, die gezählt und gemessen werden kann. Verschwindet ein Teil an einem Ort, so muss die gleiche Menge an einem andern Ort wieder auftauchen.
2. Strom und Stromdichte (Wirkung)Die zeitliche Änderung einer Erhaltungsgrösse heisst Strom ( I bzw. Φ ) . Der auf die Flächeneinheit bezogene Strom heisst Stromdichte oder Intensität.
3. Potenzial und Spannung (Ursache)Damit ein Strom fliesst, ist eine Ursache nötig. Die Ursache wird als Spannung (U) bzw. Potenzialdifferenz (U = Δφ) bezeichnet.
4. Strömungsgesetz bzw. Ursache-Wirkung-GesetzDen durch Spannungen ausgelösten Strömen stehen Widerstände (R) entgegen. Das Strömungsgesetz beschreibt den Zusammenhang zwischen Spannung und Strom, es ist in vielen Fällen linear. Der Kehrwert des Widerstandes heisst Leitwert. Der Strom fliesst immer vom höheren zu niedrigeren Potenzial. Besitzen zwei Punkte dasselbe Potenzial, so fliesst zwischen ihnen kein Strom.
5. SpeichergleichungFliesst eine Erhaltungsgrösse in einen Speicher ohne Abfluss, so wird dieser mit zunehmender Spannung geladen. Der Proportionalitätsfaktor heisst Kapazität (C). In der Praxis ist das Laden-/Entladen eines Speichers, welches vielfach exponentiellen Gesetzmässigkeiten folgt, von Interesse. Wichtige Kenngrössen des Speichers sind Zeitkonstante (τ) und Halbwertszeit (T_1 ⁄ 2).

9.1.3 Physikalische Grössen, Masseinheiten

Zur Formulierung von Zusammenhängen und Gesetzmässigkeiten bedient sich die Physik mathematischer Gleichungen, die sog. physikalische Grössen miteinander verbinden. Physikalische Grössen müssen messbar sein, sie bestehen daher aus einer quantitativen Aussage {G} (Zahlenwert) und einer qualitativen Aussage [G] (Einheit):

Um messbare Grössen zu vergleichen, sind Masseinheiten nötig. Sämtliche Einheiten lassen sich von wenigen Basiseinheiten, den sog. SI-Einheiten, die in der Vereinbarung der International Organization for Standardisation (ISO) festgelegt sind, ableiten (vgl. Anhang 9.4):

• Länge m (Meter)
• Zeit s (Sekunde)
• Masse kg (Kilogramm)
• Stoffmenge mol (Mol)
• Temperatur K (Kelvin)
• elektr. Stromstärke A (Ampere)
• Lichtstärke cd (Candela)

Grössengleichung:

• mit Begriffen: Energie = Leistung · Zeit
• mit Symbolen: E = P · t

Zugehörige Einheitengleichung:

1 Ws (Wattsekunde) = Watt · Sekunde = 1 W · 1s = 1 J (Joule)

Physikalische Einheiten lassen sich wie gewöhnliche Faktoren behandeln, d. h. sie können z. B. ausgeklammert oder gekürzt werden. Damit erlaubt die Einheitengleichung einen ersten Test, um die formale Richtigkeit einer Grössengleichung zu prüfen.

9.1.4 Material- und Zustandsgleichungen

Sie beschreiben einerseits den Zusammenhang zwischen physikalischen Grössen und Materialeigenschaften und verknüpfen andererseits Zustandsvariabeln (Grössen, die nur vom Anfangs- und Endzustand abhängen). Beispiele sind:

• Ohmscher Widerstand eines Drahtes (R_el = ρ · l/A)
• allgemeine Gasgleichung (p · V = n · R · T).

9.1.5 Die Schaltungsregeln

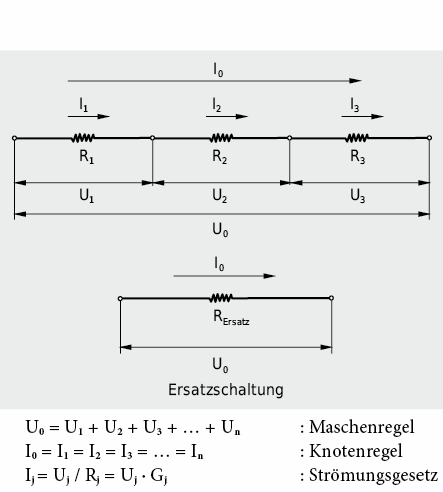
a) Serieschaltung

Der gleiche Strom fliesst verzweigungsfrei durch mehrere hintereinandergeschaltete Widerstände. Dies ist eine Folge der Kontinuitätsgleichung. Die Gesamtspannung addiert sich aus den Teilspannungen über den Widerständen. Spannungen und Widerstände sind zueinander proportional.

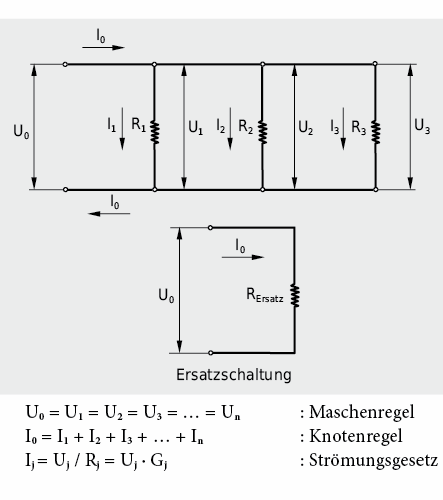
b) Parallelschaltung

Mehrere nebeneinandergeschaltete Widerstände liegen an der gleichen Spannung. Der Strom verteilt sich an der Knotenstelle, sodass der Gesamtstrom gleich der Summe der Teilströme ist. Dies ist eine Folge des Erhaltungssatzes (z. B. für Masse, Ladung, usw.). Die Ströme verhalten sich wie die Leitwerte. (PS: Bei kompressiblen Medien wie Luft stimmt der Erhaltungssatz nur für den Massestrom, nicht aber für den Volumenstrom).

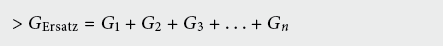
Analog zu reinen Widerstandsschaltungen lassen sich entsprechende Schaltungsregeln für Ladungsspeicher, Kapazitäten, ableiten. Die Prinzipien sind die gleichen; da eine Kapazität aber eine andere Funktionsweise als der Widerstand hat, ist das dem Element entsprechende «Funktionsgesetz», das Speichergesetz, zu verwenden:

• Serieschaltung von Kapazitäten:

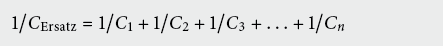
• Parallelschaltung von Kapazitäten:

Grundprinzipien, physikalische Grössen & Masseinheiten, Material- und Zustandsgleichungen bilden zusammen mit den Schaltungsregeln ein erstes, einfaches Instrumentarium zum Lösen von physikalischen Problemen.

Häufig liegen die Hauptschwierigkeiten aber nicht in der Physik selbst, sondern in der klaren Festlegung von Systemgrenzen/Randbedingungen, in der Beschaffung von zuverlässigen Daten und in der optimalen Modellierung.

9.1.6 Stationäre und instationäre Vorgänge

In der wirklichen Natur und auch am Gebäude verlaufen fast alle Vorgänge instationär, d. h. die beteiligten Betriebsvariablen wie Luftdruck, Temperatur, Feuchtigkeit, usw., aber auch Materialeigenschaften ändern sich im Lauf der Zeit. Diese zeitlichen Änderungen sind für das gedankliche Erfassen der Zusammenhänge eine Erschwerung und für eine rechnerische Abschätzung eine Komplikation.

Da in vielen Fällen die Änderungen entweder langsam verlaufen oder die Schwankungswerte gering sind, kann u. U. auf die exakte instationäre Rechnung verzichtet und bei mittleren Betriebsparametern stationär gerechnet werden. Es gibt jedoch Phänomene, bei denen der Vorgang so stark vom instationären Verlauf geprägt wird, dass eine Näherung mit konstanten Randbedingungen nicht sinnvoll ist. Das Laden oder Entladen eines Wärmespeichers ist zum Beispiel ein instationärer Vorgang, bei dem eine Mittelung zu keinen vernünftigen Aussagen über den Ladezustand führt.

Die Vielfalt der instationären Prozesse ist derart gross, dass eine systematische Behandlung nicht möglich ist. Zudem kommen wir in solchen Fällen nur mit höherer Mathematik (Differenzialgleichungen) und/oder mit Hilfe von Computerprogrammen zum Ziel. Aber das Verwenden von rechnergestützten Tools ist kein Freipass, um kritisches Denken/Analysieren auszuschalten. Lediglich bezüglich Genauigkeit, Rechengeschwindigkeit und Speicherkapazität sind die Rechner dem Menschen überlegen; die Resultate von Computerberechnungen sind nicht genauer als die Programme und Daten, mit denen sie gefüttert werden!

Ob ein Vorgang stationär oder instationär behandelt wird, ist von äusserster Wichtigkeit und Tragweite. Es hängt vom gewünschten Ziel der Berechnung ab, ob die eine oder andere Denkweise zulässig ist. Interessiert man sich z. B. bei einem vom Wind umströmten Gebäude für die mittleren Lüftungsverluste, so kann eine stationäre Rechnung für ein genügend langes Zeitintervall sinnvoll sein. Steht aber die Festigkeit einzelner Bauteile oder gar die Sicherheit des ganzen Gebäudes zur Diskussion, so muss das instationäre Verhalten des Windes unbedingt berücksichtigt werden, da eine einzige Windböe u. U. bereits zu einem Schaden führen kann. Periodische Störungen (z. B. 24h-Tagesgang der Aussenlufttemperatur) und Sprungstörungen (z. B. Ein- und Ausschaltvorgänge bei Heizungen) sind Beispiele von instationären Randbedingungen, die im Bauwesen eine zentrale Rolle spielen. Auch hier lassen sich oft einfache elektrische Analogiemodelle zum Studium und zur Lösung von z. B. thermischen, lufthygienischen oder raumakustischen Problemen heranziehen.

9.1.7 Physik – Bauphysik – Baupraxis?

Da die heute aus der Praxis zu lösenden Fragen vielfach eine starke Interdisziplinarität zeigen, kommt dem Praxisbezug der Physik als Grundlagenwissenschaft und der Zusammenarbeit mit anderen Disziplinen eine zentrale Rolle zu. Einerseits wird es notwendig sein, physikalische Modelle, Theorien, Gesetze, aber auch Arbeitsmethoden der Physik zum Verständnis von Phänomenen und Prozessen in der Natur und der bebauten Umwelt heranzuziehen. Andererseits ist ein praktisches, «reales» Problem zu Beginn meist nicht streng physikalisch- mathematisch lösbar. Die Aufgabe muss zuerst «idealisiert», d. h. in eine Fragestellung umgewandelt werden, in der quantitativ bzw. mindestens qualitativ beschreibare physikalische Grössen vorkommen. Diese Umwandlung nennen wir Modellierung. Erst das von «Nebensächlichkeiten» befreite Problem kann nun nach physikalischen Methoden untersucht werden. Hat sich das Modell (bzw. die Hypothese) reproduzierbar in jeder Richtung bewährt und ist es quantitativ, meist mit Hilfe mathematischer Methoden, erfassbar, so sprechen wir von einer Theorie. Die Lösung des rein physikalischen Problems muss durch Experimente/Messungen verifiziert, anschliessend im Hinblick auf die «reale» Fragestellung interpretiert und u. U. durch realitätskonforme, praxistaugliche Anpassungen ergänzt werden.

Diese Arbeitsmethodik, dieser Kreislauf

• Beobachtung/Analyse
• Modellbildung
• Theorie
• Verifizierung
• Korrektur/Anpassung

gilt sowohl für «idealisierte» physikalische Phänomene wie für «reale» baubezogene Prozesse.