9 Anhang

9.2.1 Kreis, Kugel und Kreiszylinder

9.2.2 Quadratische Gleichung

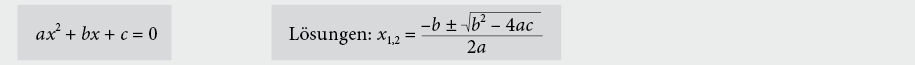
9.2.3 Binomische Formeln

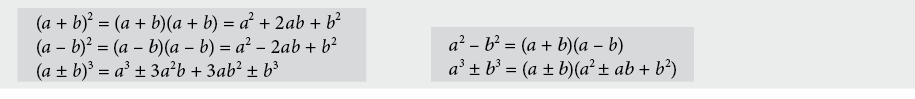
9.2.4 Lineare Funktion und Geradengleichung

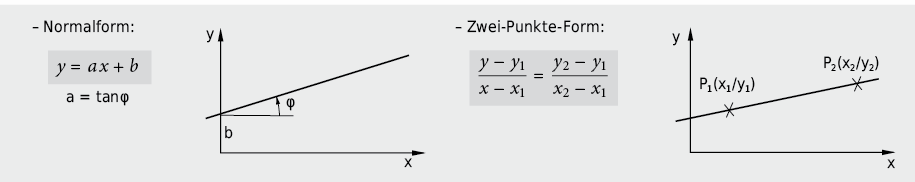
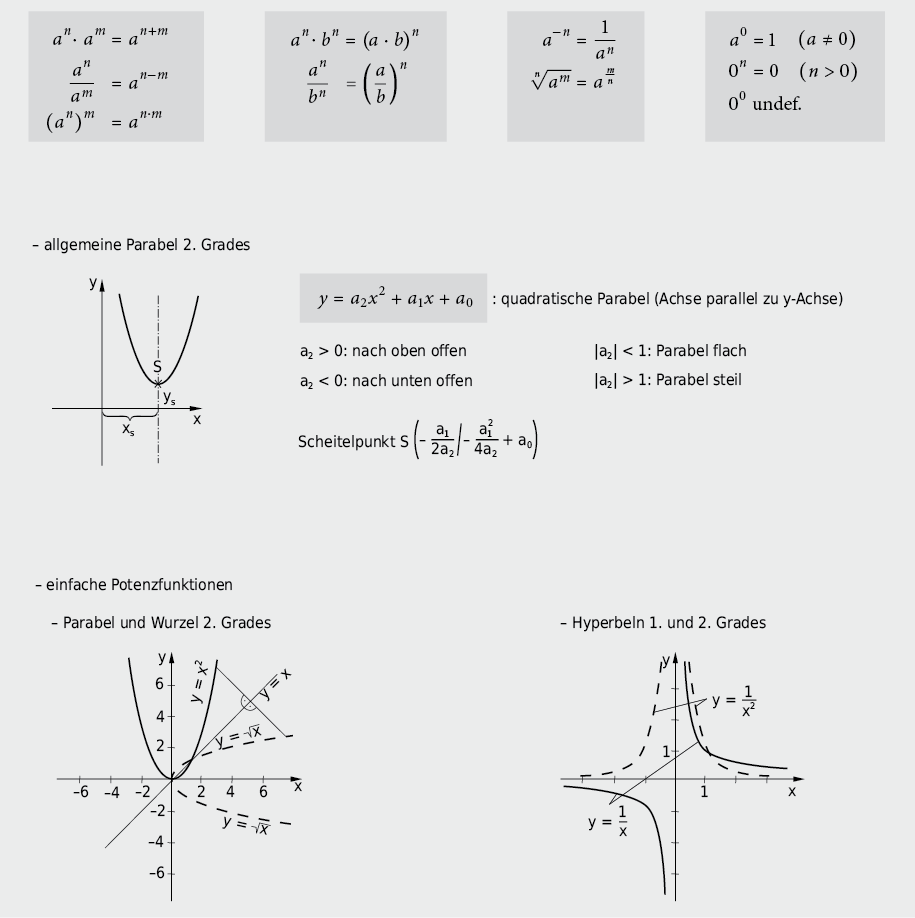
9.2.5 Potenzgesetze und Potenzfunktionen

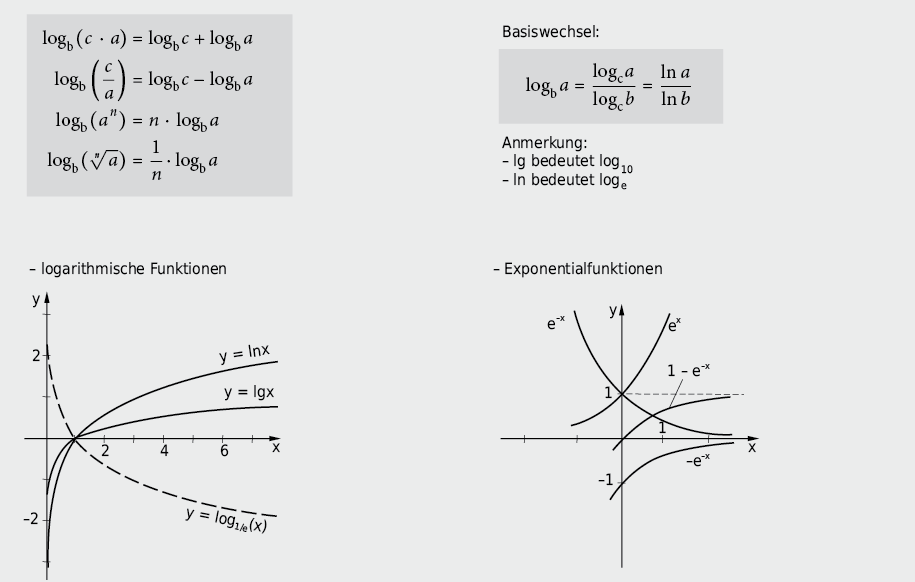
9.2.6 Logarithmengesetze und Logarithmus-/Exponentialfunktionen

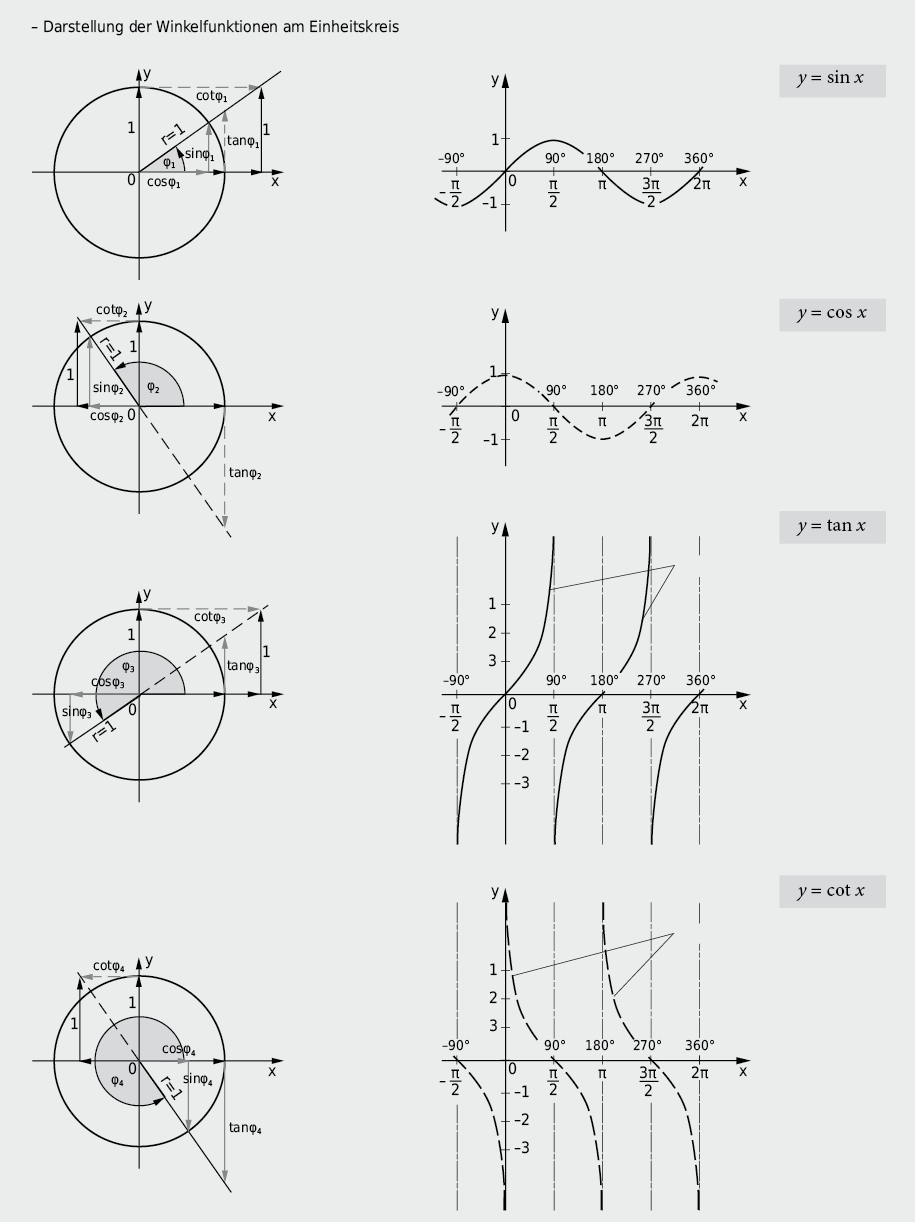
9.2.7 Dreieck und Winkelfunktionen

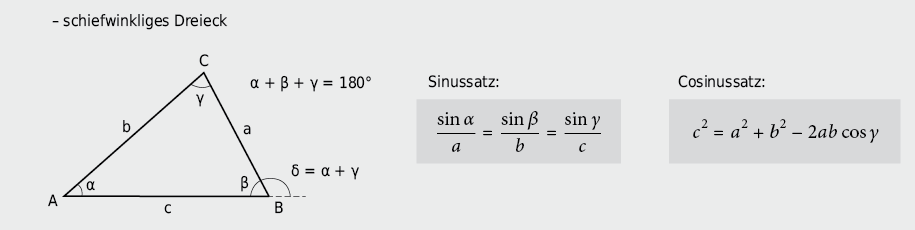
9.2.8 Ableitung und Integrale

9.2.9 Reihenentwicklungen

9.2.10 Vektorprodukte

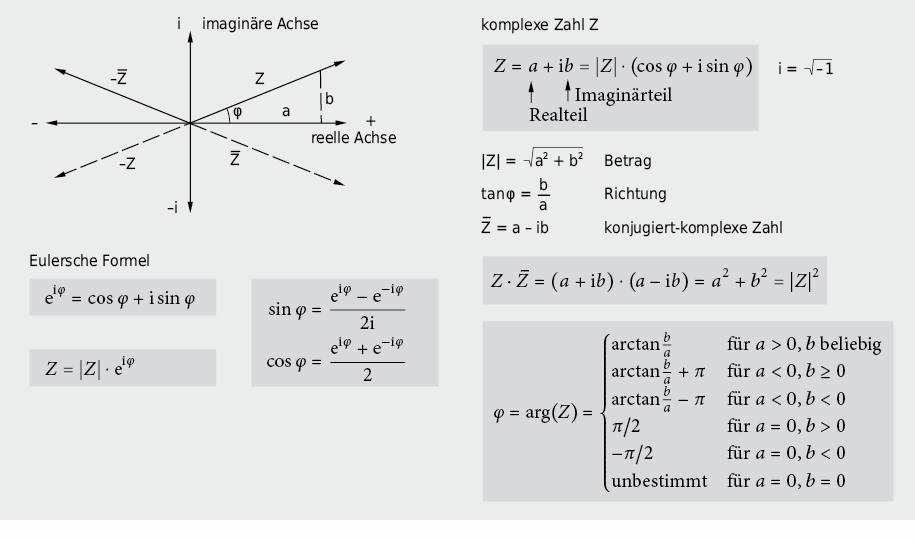
9.2.11 Komplexe Zahlen

9.2.12 Messungen und deren Auswertung

Bereits in der Phase der Planung von Messungen sind die Gesetzmässigkeiten der Fehlerrechnung beizuziehen und zu prüfen, wie sich einzelne Unsicherheiten/Fehlerbeiträge – systematische wie zufällige – auf die zu messende Grösse auswirken. Vor der Messung ist zu entscheiden, wo, wie und mit welchem Aufwand und Ziel Fehler verringert, womöglich eliminiert werden können bzw. sollen.

Zufällige Fehler

Schwankungen von Messwerten als Folge von Zufallseffekten werden als zufällige Fehler (engl.: random errors) bezeichnet. Mit zufälligen Fehlern behaftete Messgrössen gehorchen im Allgemeinen einer Normal-(Gauss-)Verteilung.

Mittlere Fehler einer Messgrösse

Eine Grösse µ werde n-mal unter möglichst gleichbleibenden Bedingungen gemessen, die n Messwerte x_j (j = 1 …n) stellen eine Stichprobe (engl.: sample) der Grundgesamtheit (engl.: population) dar. Nach Gauss ist der arithmetische Mittelwert x (engl.: arithmetic average) die beste Näherung (auch Schätzwert, engl.: estimate, genannt) für den Erwartungswert µ (engl.: expectation value, auch wahrer Wert genannt):

Die Standardabweichung s der Stichprobe (ISO: experimental standard deviation) bzw. deren mittlerer Fehler beträgt

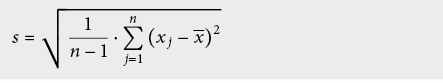
Sie charakterisiert die Genauigkeit des gewählten Messverfahrens und kann deshalb durch Wiederholungsmessungen nicht verbessert werden; dazu müsste das Messverfahren geändert werden.

Hingegen lässt sich die statistische Unsicherheit des Mittelwertes, sog. Standardabweichung des Mittelwertes s_m (ISO: experimental standard deviation of the mean) durch Wiederholung von Messungen verkleinern:

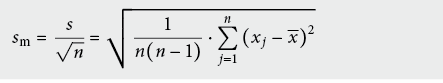
s_m ist ein Mass für die Abweichung zwischen Schätzwert x und Erwartungswert µ.

Bei kleiner Anzahl von Messungen ist eine Normalverteilung meist schwer nachweisbar und die Abschätzung des Erwartungswertes dementsprechend ungenau, sodass die Güte der Abschätzung durch einen Vertrauensbereich (engl.: range of confidence) um den arithmetischen Mittelwert charakterisiert werden muss:

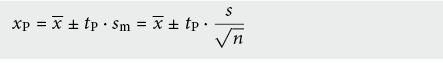
Der « Vertrauensfaktor » t_P hängt von der Anzahl Wiederholungsmessungen n_w (Anzahl Messungen N minus Anzahl gesuchte Erwartungswerte k) und der geforderten statistischen Sicherheit P (Sicherheit in %, dass der Vertrauensbereich den wahren Wert umfasst) ab:

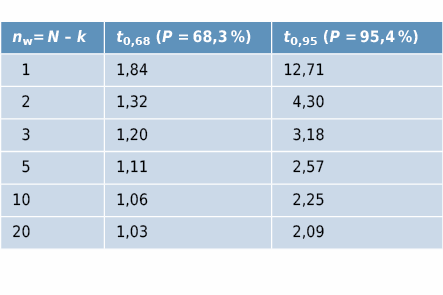
Fehlerfortpflanzung bei mehreren Messgrössen

Kann eine physikalische Grösse f (x, y, z, …) nicht direkt, sondern nur über Messungen der Teilgrössen x, y, z, … bestimmt werden, so ist der wahrscheinlichste Wert gleich dem Funktionswert mit den Mittelwerten

Die Standardabweichung s–_f der Grösse f berechnet sich nach dem Gauss ’schen Fehlerfortpflanzungsgesetz zu:

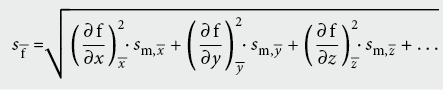
Mit Hilfe der absoluten bzw. relativen maximalen Fehler der Teilgrössen lässt sich die Grössenordnung des Fehlers in einer ersten Phase meistens einfacher abschätzen, jedoch erhält man so nur eine Aussage über den Maximalfehler (Fehlerschranken):

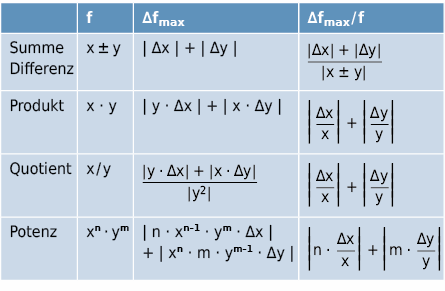
Systematische Fehler

Diese Art Messfehler (engl.: systematic error), die trotz variierten Messbedingungen immer wieder gleiche Werte – sowohl bezüglich Grösse wie Vorzeichen – ergeben, lassen sich durch Wiederholung weder erkennen noch verringern bzw. eliminieren. Sie lassen sich allenfalls durch Änderung der Messmethode korrigieren.

Liegt neben den zufälligen Fehlern eine systematische Messunsicherheit vor, so ist als Gesamt-Messunsicherheit einer Teilmessung die Summe der entsprechenden Unsicherheiten anzugeben.

Für eine Funktion f = f (x, y, z, …), deren Teilgrössen mit systematischen Fehlern h_j (j = x, y, z, …) behaftet sind, pflanzen sich die Fehler wie folgt fort:

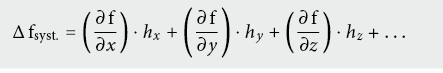
Im Gegensatz zu den Zufallsfehlern, wo sich die Quadrate der Beiträge der Messgrössen wie orthogonal stehende Vektoren addieren, sind systematische Fehlerbeiträge algebraisch zu addieren.

Ausgleichung bei funktionalen Zusammenhängen (Regressionsanalyse)

Wird ein linearer Zusammenhang y = ax + b zwischen der Messvariablen x und der Messgrösse y erwartet, so lassen sich die Parameter Steigung (a) und Achsenabschnitt (b) durch Ausgleichung nach dem Prinzip der kleinsten Quadrate (engl.: least square) bestimmen:

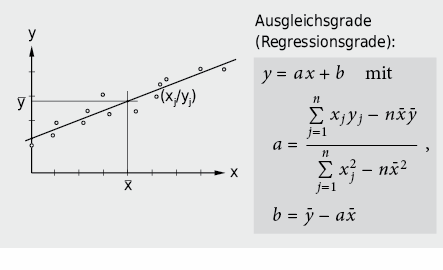
Oft lässt sich eine nicht lineare funktionale Beziehung durch geeignete Variablentransformation linearisieren:

• Exponentialfunktionen durch einfach-logarithmische Darstellung (y → lny)
• Potenzfunktionen durch doppelt-logarithmische Darstellung (x → logx und y → logy)

Dabei gilt es zu beachten, dass allfällige Gewichte g_j der einzelnen Messwerte entsprechend der Transformation anzupassen sind.

Weiterführende Literatur zum Thema

W. H. Gränicher, Messung beendet – was nun? Einführung und Nachschlagewerk für Planung und Auswertung von Messungen, vdf Hochschulverlag AG an der ETHZ, Zürich (1996)