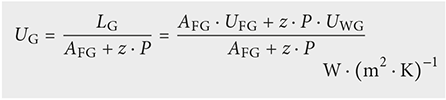Les ponts thermiques sont des emplacements ou des régions de l’enveloppe du bâtiment où l’on observe des perturbations locales des flux thermiques et des températures par rapport au cas d’une transmission thermique unidimensionnelle. On peut distinguer les trois situations suivantes:
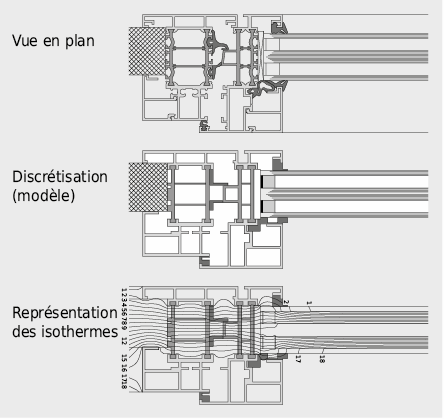
- les ponts thermiques matériels qui se produisent sur des discontinuités partielles ou complètes dans l’enveloppe thermique par des matériaux ayant des conductivités thermiques différentes comme, par exemple, les cadres de fenêtre (voir Fig. 2.42).
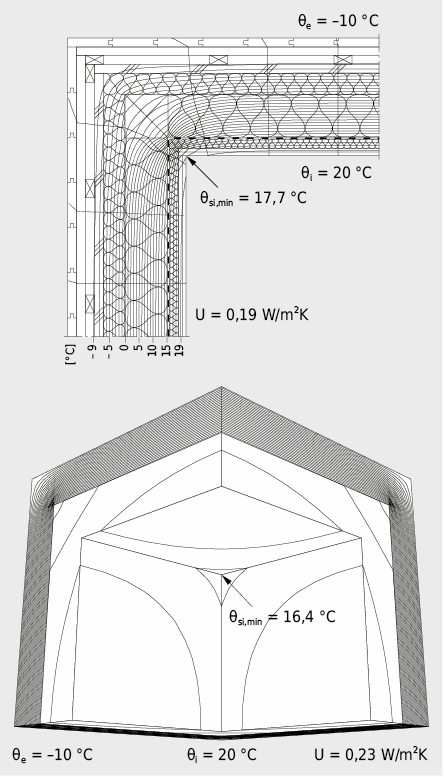
- les ponts thermiques géométriques qui se produisent par une variation dans l’épaisseur d’un élément ou lorsque ses dimensions intérieures et extérieures diffèrent comme, par exemple, les coins de murs (voir Fig. 2.43).
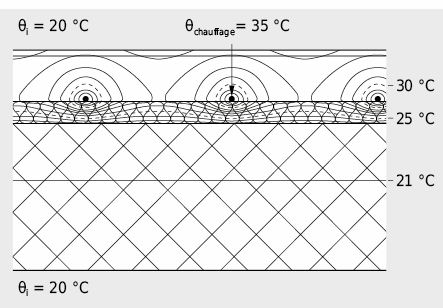
- des conditions aux limites localement différentes, par exemple des sources de chaleur par les tubes d’un chauffage au sol (voir Fig. 2.44).
Uf = 1,66W · (m2 · K)–1
Ug = 0,5W · (m2 · K)–1
Ψg = 0,077W · (m · K)–1
Bien que l’on ne puisse pas éliminer entièrement les ponts thermiques, il est cependant nécessaire de limiter, autant que possible, leurs effets sur la transmission thermique et les températures de surface. C’est pourquoi, dans la phase de planification, il faut identifier les emplacements critiques de l’enveloppe du bâtiment et les étudier avec des méthodes appropriées. Ces diverses méthodes sont disponibles:
- méthodes de calcul approximatif
- catalogues de ponts thermiques [2.11]
- méthodes de calcul numérique (méthodes des différences finies et des éléments finis)
- mesures en laboratoire (méthode de la boîte chaude, observation par thermographie)
2.3.1 Méthode d’approximation pour les éléments de construction plans
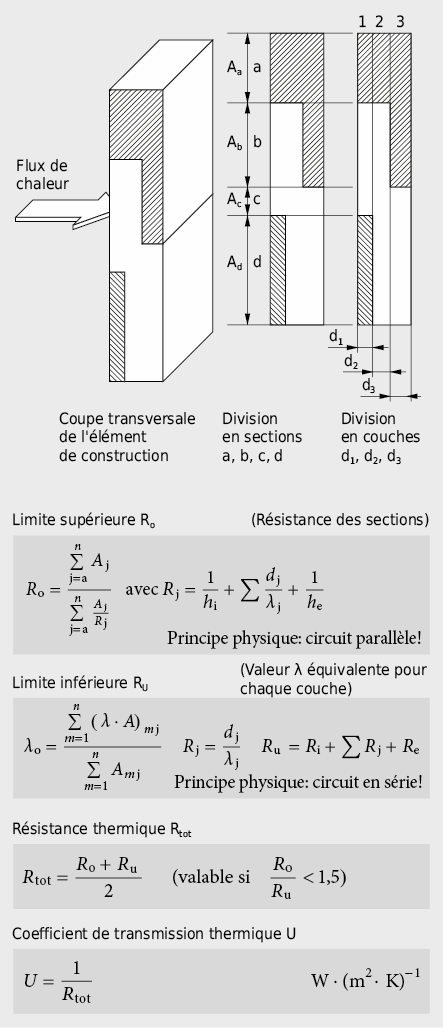
La résistance thermique R d’un élément de construction plan inhomogène peut être évaluée par une méthode d’approximation. L’élément est décomposé verticalement en sections et horizontalement en couches afin d’obtenir une valeur limite spérieure et une valeur limite inférieure de la résistance thermique (voir [2.3]).
2.3.2 Méthodes numériques
Pour étudier les ponts thermiques, des méthodes numériques bidimensionnelles ou tridimensionnelles (méthodes par différences finies et par éléments finis) sont employées [2.21]. Ces procédures numériques nécessitent une discrétisation de l’objet étudié. Concrètement un modèle 2D ou 3D est établi, généralement sous la forme d’un réseau de mailles rectangulaires. Pour chaque noeud du réseau, respectivement chaque élément du maillage, un bilan des flux thermiques est posé.
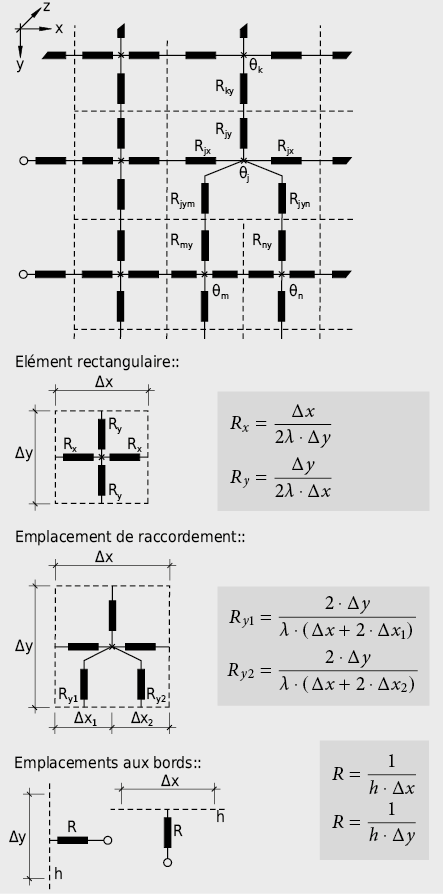
Le système d’équations obtenu de cette manière est résolu soit par itérations soit par une méthode de résolution directe. La finesse de la discrétisation de l’objet doit être choisie de manière à ce que la somme des valeurs absolues de tous les flux de chaleur qui s’écoulent dans l’objet atteigne une valeur convergente. Selon EN ISO 10211 [2.22], un doublement des subdivisions ne doit pas provoquer des variations de plus de 1 % sur les flux thermiques et de 0.005 sur les facteurs de température superficielle fRsi. Si le système d’équations est résolu par itérations, celles-ci sont poursuivies jusqu’à ce qu’une divergence suffisamment réduite soit atteinte (< 0,1 %).
Le flux thermique Φ déterminé par des méthodes numériques pour un local ou un bâtiment peut être représenté de la façon suivante:

Si le local ou le bâtiment sont décomposés en plusieurs sous-domaines (surfaces planes, coins bidimensionnels ou tridimensionnels, etc.), la valeur totale Li,j se calcule comme:
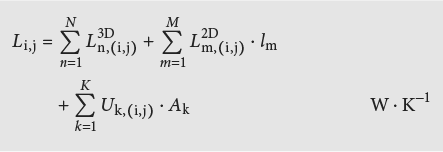

La signification des conductances thermiques dans des conditions aux limites avec plusieurs températures est illustrée à la figure 2.47.

2.3.3 Isothermes, facteurs de température superficielle
Quand, après plusieurs itérations, la précision exigée est atteinte pour la température de chaque noeud, il est possible de tracer ce que l’on dénomme les isothermes (lignes de température constante) sur la coupe de l’élément. A partir du champ d’isothermes, le cheminement du flux de chaleur peut ensuite être simplement déterminé car toutes les lignes de flux croisent toujours les isothermes à angle droit.
θe = –15 °C θi = +20 °C
he = 20 W · (m2 · K)–1 hi = 6 W · (m2 · K)–1
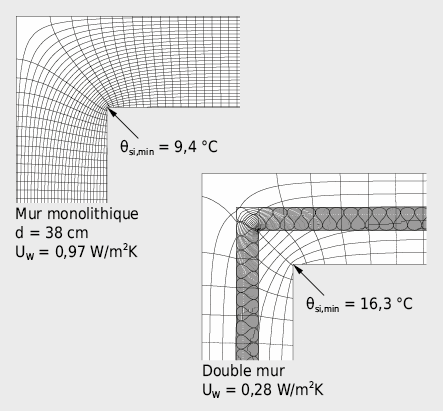
Les figures 2.43 et 2.48 montrent clairement que les coins refroidissent plus à cause de leurs plus grandes surfaces exposées vers l’extérieur ce qui se traduit par une baisse marquée de leur température θsi, min par rapport à la température de surface θsi dans la coupe transversale typique. Par la disposition d’une couche d’isolation thermique intermédiaire dans le mur en brique, la température de surface critique dans le coin augmente de ≈ 9 °C à 16 °C (voir Fig. 2.48). Toutefois, l’effet de pont thermique géométrique demeure.
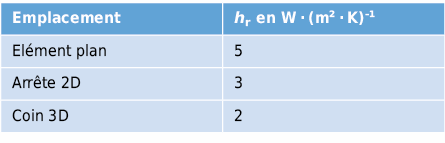
Les températures de surface minimales sont fortement influencées par les conditions de transfert de chaleur sur les surfaces intérieures. Sur les arrêtes et les coins, les échanges par rayonnement sont réduits. Les coefficients de transfert surfacique par rayonnement indiqués au tableau 2.17 peuvent être employés.
La température de surface locale θsi au point x,y,z peut être calculée de la manière suivante avec les deux températures des conditions aux bords:

En présence de conditions aux bords comprenant plus de deux températures, la température de surface peut être déterminée comme suit:

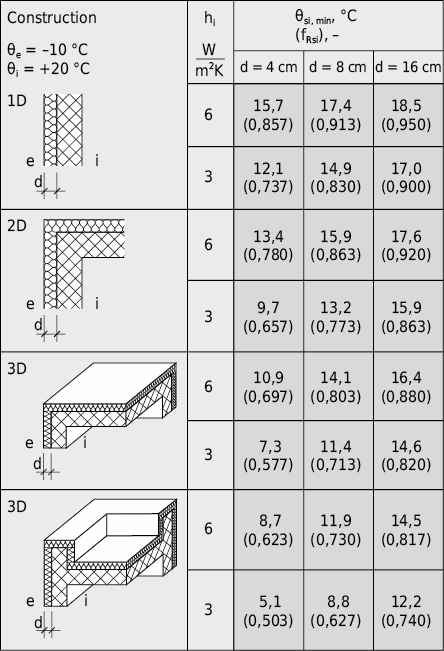
La figure 2.50 présente les températures de surface minimales θsi,min ainsi que les facteurs de température superficielle fRsi correspondants pour quelques constructions typiques et pour différents coefficients de transfert de chaleur surfacique.
2.3.4 Majorations pour ponts thermiques linéaires et ponctuels
Pour les applications pratiques, les déperditions thermiques supplémentaires provoquées par un pont thermique sont déterminées relativement simplement par majoration Ψ pour pont thermique linéaire ou χ pour pont thermique ponctuel.
La conductance thermique totale Li,j s’obtient en utilisant ces facteurs de majoration de la façon suivante:

Les majorations dues aux ponts thermiques sont déterminées comme suit:
- pour un élément – 2D
- flanquant un élément – 3D central

- pour un élément – 3D central
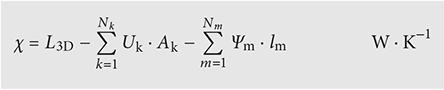
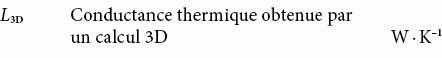
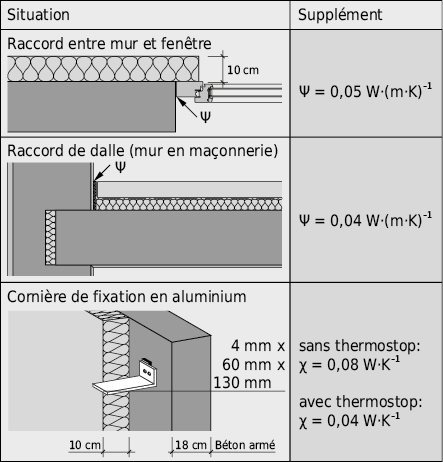
2.3.5 Valeur U moyenne
Pour une partie de l’enveloppe du bâtiment ou pour son ensemble, une valeur U moyenne peurt être définie pour autant que tous les éléments soient soumis au même écart de température. La valeur U moyenne Um doit comprendre l’esemble des facteurs de déperdition, c’est-à-dire tous les ponts thermiques (linéiques ou ponctuels) existants.

2.3.6 Déperditions thermiques dans le terrain
Les transferts de chaleur autour des éléments de construction enterrés se font de manière multidimensionnelle. L’influence du climat extérieur est amortie et différée dans le temps par les couches de terre [2.31]. Les propriétés de conductivité thermique varient dans les plages suivantes selon la nature du sol:
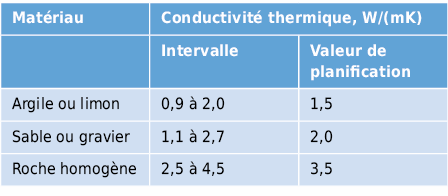
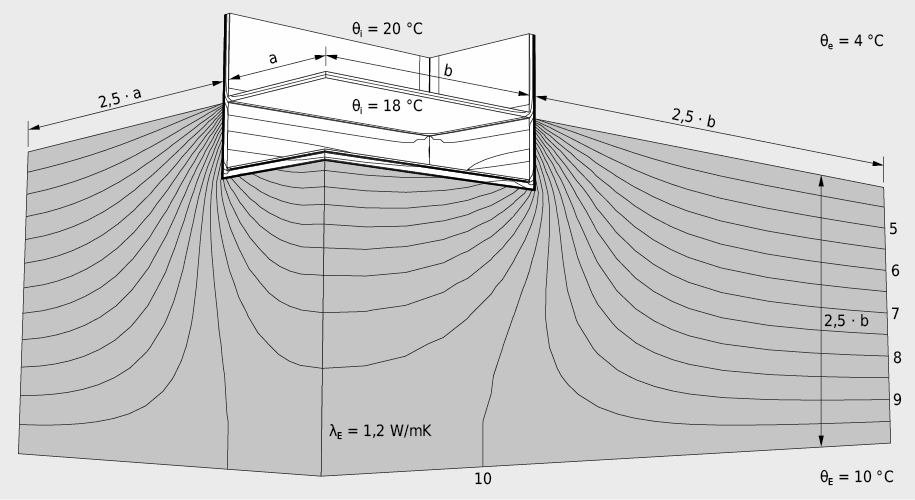
Comme on le voit sur la répartition des isothermes illustrée à figure 2.53, les plus importantes déperditions thermiques se produisent dans la région du périmètre, c’est-à-dire le long des surfaces délimitant le bâtiment. Ainsi, les mesures d’isolation thermique doivent avant tout concerner les murs. Pour le radier, les conditions aux limites spécifiques du lieu et de l’objet doivent être incluses dans l’évaluation:
- Profondeur sous la surface du terrain
- Nature du sol et conditions d’humidité (couches aquifères)
- Taille de la surface occupée au sol par le bâtiment
Dans l’agencement de mesures d’isolation thermique, le risque de dommages dus au gel (soulèvement par le gel et infiltrations d’eau) doit être clarifié.
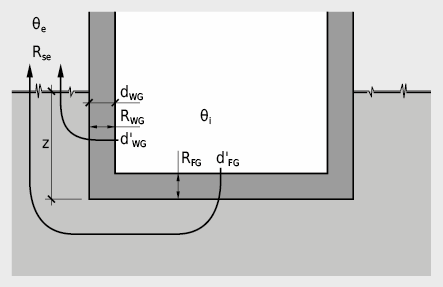
Pour les calculs de flux thermiques, les dimensions de terrain indiquées à la figure 2.53 doivent être considérées [2.23].
En moyenne annuelle, la puissance des pertes thermiques d’une cave chauffée peut être déterminée selon EN ISO 13370 [2.23] de la manière suivante:

La conductance thermique se compose d’une part concernant le mur et d’une autre part concernant le radier:

Comme il s’agit d’un transfert de chaleur qui s’opère dans une situation tridimensionnelle, les dimensions de la cave doivent être prises en compte. Dans ce but on introduit une « dimension caractéristique » du radier:

Les résistances thermiques du mur et du radier sont traitées à l’aide du «concept d’épaisseur équivalente », c’est-à-dire l’épaisseur d’une couche de terre qui présente une résistance thermique identique. Les définitions des épaisseurs équivalentes pour le radier dʹFG et pour le mur dʹWG sont les suivantes:

Les coefficients de transmission thermique du radier et du mur sont déterminés selon EN ISO 13370 [2.23]:

Le coefficient de transmission thermique U effectif de la cave vers le climat extérieur vaut: