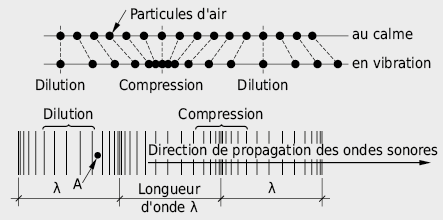
Sous le terme son on comprend des vibrations et leur propagation sous forme d’ondes longitudinales dans un milieu élastique. Les particules déplacées par les vibrations bougent en avant et en arrière dans le sens de propagation.
Les fluctuations de pression ainsi créées peuvent se propager tant dans les corps solides sous forme de ce que l’on dénomme son solidien que dans l’air sous forme de son aérien. Les signaux acoustiques que l’oreille humaine perçoit comme un son ou une pression acoustique sont de petites fluctuations de la pression de l’air qui s’ajoutent à la pression atmosphérique (pression barométrique).
De telles oscillations de pression représentent une perturbation du milieu élastique et se propagent sous forme d’ondes sonores avec une vitesse caractéristique du milieu appelée célérité du son c. La formule suivante peut être employée comme approximation pour la célérité du son c dans l’air:

Dans les corps solides on peut admettre en première approximation:

Le nombre d’oscillations que fait une particule de matériau chaque seconde est décrit par la fréquence f (nombre d’oscillations 1 s–1 ≙ 1 Hz).

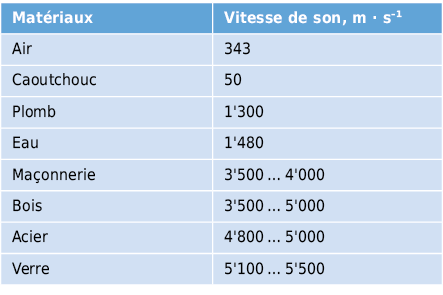
La distance minimale entre deux particules qui se trouvent dans le même état d’oscillation se dénomme longueur d’onde λ en m.
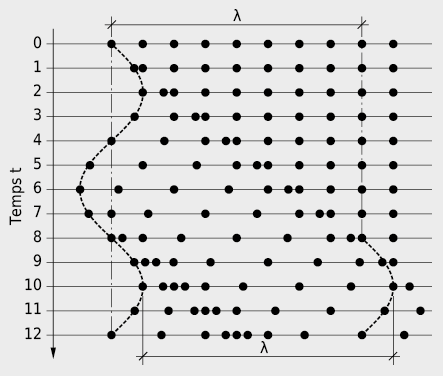
La relation entre les états de pression dans l’espace et le temps lorsque le son se propage est fournie par l’équation d’onde. Pour une équation d’onde plane, la solution s’écrit:
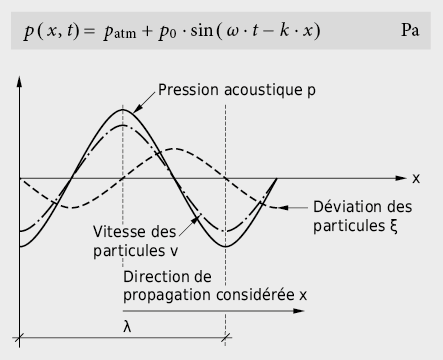
avec 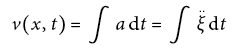 on a:
on a:

Entre la vitesse de propagation c, la fréquence f et la longueur d’onde λ d’une onde, il existe une relation fondamentale:

Lors de la propagation d’une onde dans divers milieux, la fréquence f demeure constante tandis que la vitesse de propagation c et la longueur d’onde λ changent aux interfaces entre milieux.
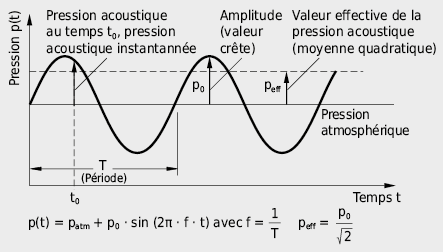
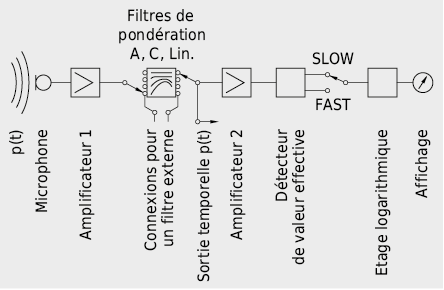
Les capteurs de son ne captent pas la pression acoustique p(t) instantanée, mais – de façon analogue au courant alternatif – la valeur effective de la pression acoustique peff qui correspond à la moyenne quadratique temporelle de la pression acoustique instantanée p(t). Elle est définie de la façon suivante:

Pour une oscillation de pression idéalisée de forme sinusoïdale on obtient par conséquent:

Le domaine dynamique de la valeur effective peff , dans lequel l’oreille humaine peut percevoir les fluctuations de pression comme des sons, est très large (voir aussi Fig. 7.7):
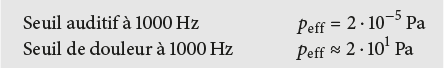
(en comparaison:
pression acoustique moyenne à Zürich ≈ 95’000 Pa!)
Contrairement à la célérité du son c qui décrit la propagation d’une onde de pression de particules à particules, on comprend sous la dénomination de vitesse acoustique des particules v la vitesse avec laquelle chaque particule de matériau vibre autour de sa position de repos dans le champ sonore. Pression acoustique et vitesse acoustique des particules sont proportionnels entre elles. Leur rapport est indépendant du lieu et du temps.

Ce rapport entre une cause déclencheuse (pression) et la vitesse des particules (vitesse acoustique des particules) induite est décrite comme impédance acoustique caractéristique Z (résistance acoustique).

La grandeur Z a une influence déterminante sur la réflexion des ondes acoustiques sur les surfaces et aux interfaces entre milieux (voir section 7.2.1).
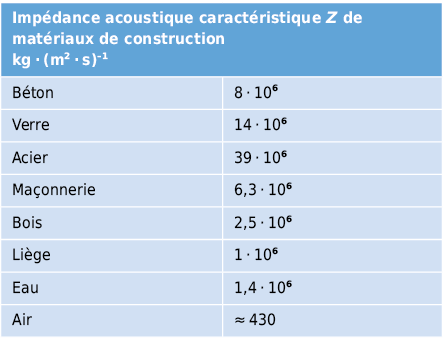
Cette grandeur assez peu parlante joue un rôle important pour l’estimation de l’insonorisation. Cette dernière est d’autant meilleure que les impédances acoustiques des deux milieux attenants sont différentes. De là découle déjà une simple règle du pouce: on peut amortir efficacement le son aérien avec des corps lourds et le son solidien avec des cavités d’air entre deux parois. Si plusieurs matériaux de même impédance sont contigus, alors le son passe sans affaiblissement.
Avec l’onde qui se propage, de l’énergie mécanique est évacuée de la source de nuisance et répartie dans la pièce. Il est ainsi intéressant d’employer, à la place de la pression acoustique, l’intensité sonore
I c’est-à-dire l’énergie sonore dW traversant un élément de surface dA pendant un intervalle de temps dt:

En raison de la très large plage de travail de l’oreille humaine et de son traitement logarithmique du stimulus sonore (loi de Weber-Fechner), il est nécessaire de disposer de certaines grandeurs caractéristiques du champ sonore en échelle logarithmique (voir Fig. 7.5). Ainsi le niveau de pression acoustique Lp et le niveau d’intensité acoustique LI sont définis de la manière suivante:
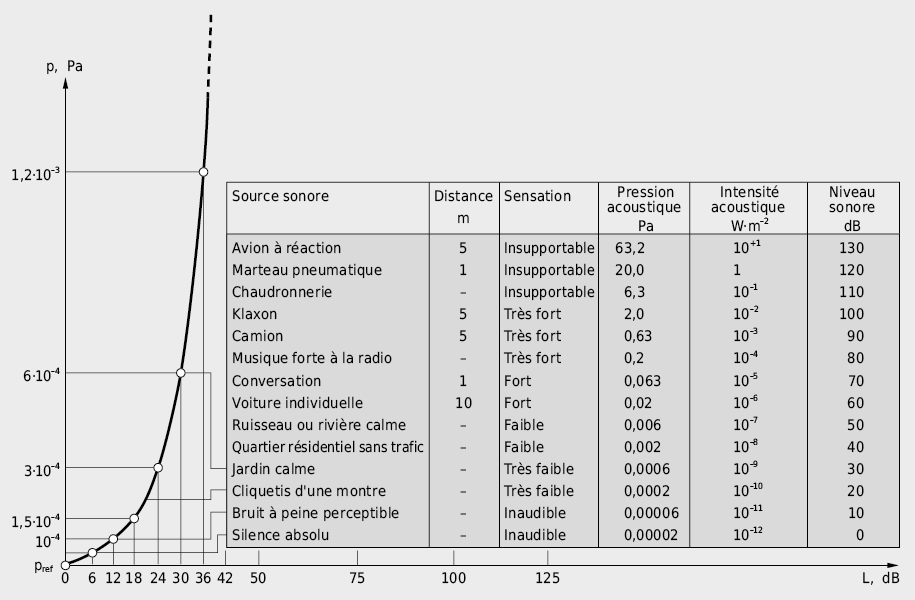

Le niveau d’intensité acoustique respectivement le niveau de pression acoustique est strictement une grandeur sans dimension. L’unité décibel (dB) a simplement été rajoutée pour indiquer la méthode de calcul utilisée. La définition logarithmique réduit l’énorme domaine des intensités audibles d’environ 12 ordres de grandeurs à une échelle comprenant 120 niveaux de dB. Le niveau sonore est une grandeur relative, déterminée par rapport à un niveau de référence I0 ou p0. Une pression acoustique p0 respectivement un niveau de pression acoustique de 0 dB correspond à peu près au niveau du seuil auditif.
Pour la description des sources sonores et de leurs émissions sonores, on fait appel à la puissance acoustique qui, en référence aux niveaux sonores définis plus haut, est aussi décrite logaritmiquement par ce que l’on appelle le niveau de puissance acoustique LW avec une puissance acoustique de référence P0 :

Les deux précédentes grandeurs sont invariantes par rapport aux propriétés acoustiques de l’entourage de la source sonore et au type de propagation de l’énergie sonore.
Addition de niveaux de pression acoustique
Deux niveaux sonores s’additionnent « selon leurs intensités » et pas algébriquement en dB!

L’addition de deux niveaux présente au maximum une élévation de 3 dB dans le cas où les deux niveaux à additionner sont identiques. Plus les niveaux à additionner diffèrent entre eux, plus l’élévation « additive » du niveau le plus élevé devient petite. Lorsque la différence de niveaux atteint 10 dB, la « correction additive » ne vaut plus que 0,4 dB.
L’addition de deux niveaus de pression acoustique L1, L2 peut être simplifiée de la manière suivante:
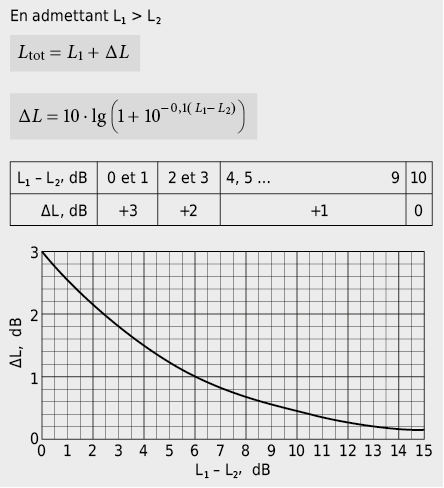
Souvent une valeur moyenne temporelle est indispensable pour décrire un évènement sonore. Le niveau moyen Leq , aussi appelé niveau sonore équivalent, est défini de la façon suivante:

Les ondes sonores qui parviennent à l’ouïe produisent une sensation de son dans laquelle on distingue la hauteur tonale, le timbre et l’intensité acoustique.
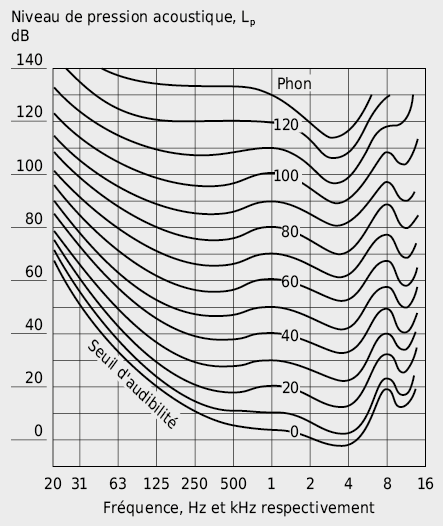
L’oreille humaine perçoit les bruits dans une plage de fréquences qui s’étend d’environ 16 à 16’000 Hz. Toutefois sa sensibilité dépend tant de la fréquence que de l’intensité du son incident.
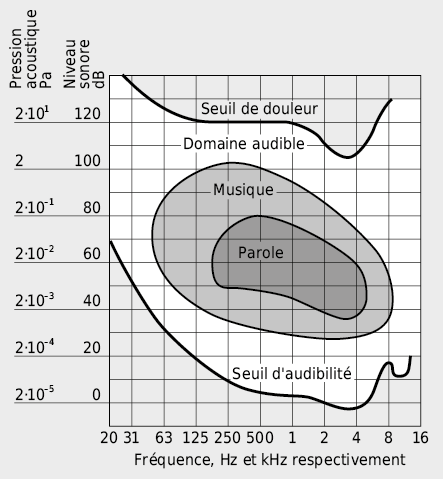
La plage entre le plus petit niveau sonore encore perceptible (seuil auditif) et le niveau perceptible maximal (seuil de douleur) est décrit comme le domaine audible. A environ 1000 Hz le seuil auditif se situe à environ 0 dB et augmente, pour les fréquences inférieures, jusqu’à 70 dB. Le seuil de douleur à 1000 Hz se situe à environ 120 dB.
Par conséquent, il ne suffit pas de décrire un son (bruit) uniquement par l’évolution temporelle du niveau de pression acoustique; des informations détaillées sur la répartition et l’intensité des fréquences présentes dans un bruit sont beaucoup plus nécessaires. Ce que l’on dénomme analyse fréquentielle fournit, à partir de l’évolution temporelle de la pression acoustique de n’importe quel signal acoustique, la répartition des intensités sonores en fonction de la fréquence (→ spectre de fréquence, voir Fig. 7.9 et 7.10).
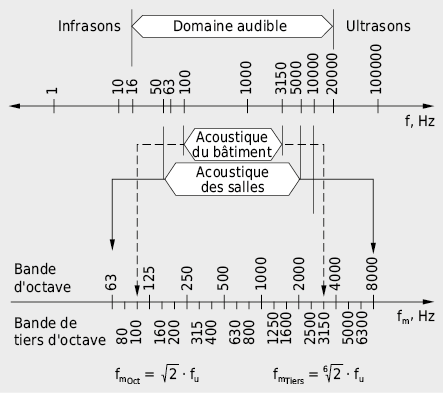
Dans la représentation en spectre de fréquence, l’ensemble du domaine des fréquences intéressantes (environ 16 Hz–16 kHz) est subdivisé en bandes individuelles à l’aide de filtres qui, chacun, ne laisse passer qu’une plage de fréquences précisément délimitée. En général une répartition logarithmique qui compresse le domaine des fréquences avec une résolution régulière permet une meilleure lisibilité.
Dans une analyse par bandes d’octave, les fréquences limites (fréquence limite inférieure (fu), supérieure (fo)) ont un rapport de 1:2 alors que dans une plus fine analyse par tiers d’octave, on a 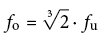 .
.
Pour l’insonorisation des bâtiments, la plage de fréquence la plus importante se situe à peu près entre 100 Hz et 3200 Hz (un domaine dans lequel l’oreille humaine est la plus sensible et où la part de l’intensité sonore des sons usuels est la plus forte; voir Fig. 7.8).
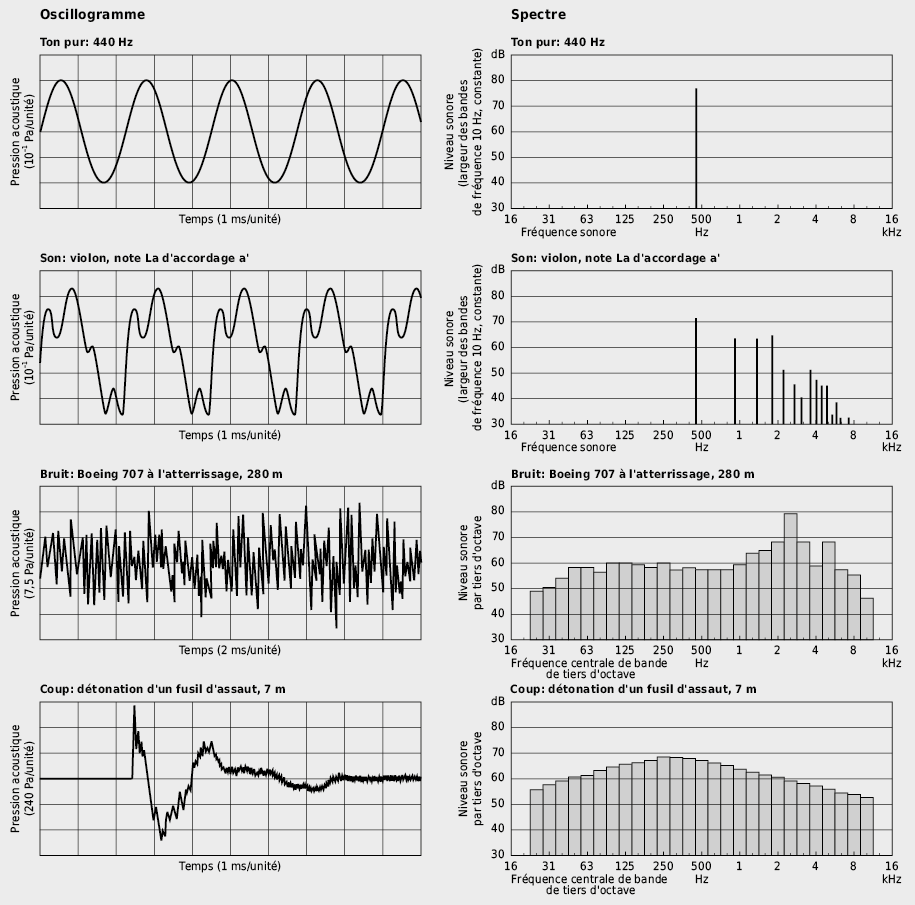
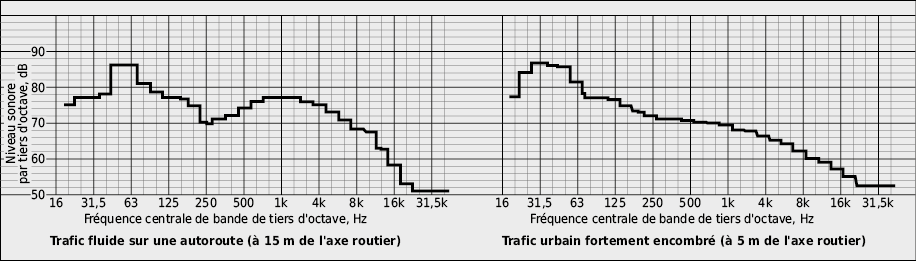
Dans l’analyse de systèmes acoustiques, ce que l’on dénomme bruit blanc est souvent employé. Ce type de bruit a une densité de puissance dl/df constante. En le filtrant par octave, son niveau augmente de 3 dB à chaque octave alors qu’avec un filtrage par tiers d’octave, le niveau augmente de 1 dB à chaque tiers.
Pour l’étude acoustique des bâtiments, on fait appel au bruit rose. Dans un bruit rose, la densité de puissance décroît à mesure que la fréquence augmente. Une analyse par octave ou tiers d’octave présente dans chaque bande le même niveau.
Des sons de fréquences différentes mais qui ont des niveaux de pression acoustique identiques ne sont pas perçus par les personnes comme ayant la même force. Le niveau de pression acoustique objectif L en dB ne suffit ainsi pas pour caractériser l’effet subjectif d’un son. C’est ce que l’on appelle l’intensité sonore qui décrit le niveau sonore tel que ressenti de sons ayant des fréquences différentes (voir Fig. 7.11).
Les courbes d’égale intensité sonore LS en phon indiquent, pour des sons purs, le niveau sonore qui, pour la fréquence correspondante, est ressenti aussi fortement qu’un son à 1000 Hz de pression acoustique déterminée.
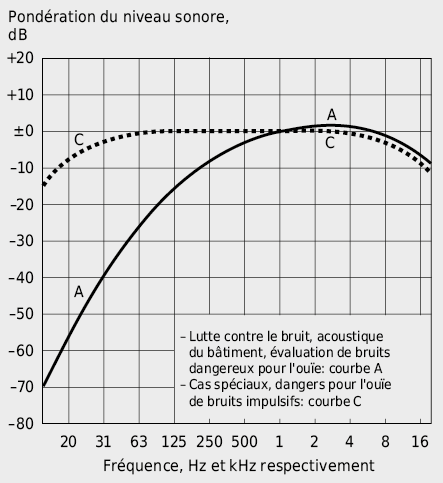
Pour que les mesures sonores correspondent à la sensibilté humaine au bruit, les valeurs mesurées doivent être corrigées selon les différentes gammes de fréquence. Les instruments de mesure sont pour cela équipés de filtres de pondération qui atténuent ou amplifient le signal selon les courbes fréquentielles de pondération (voir Fig. 7.12 et 7.13).
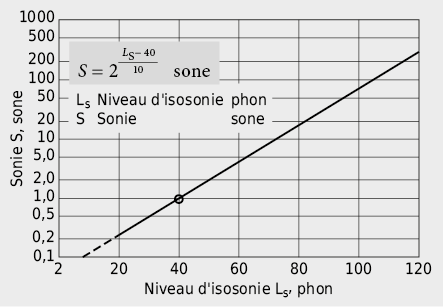
Pour les applications pratiques, ces relations relativement peu commodes et compliquées autour de la perception de l’intensité sonore peuvent être simplifiées en employant ce que l’on dénomme la sonie S en sone plutôt que le niveau d’intensité sonore LS en phon pour décrire la perception subjective de l’intensité sonore. A l’aide de la loi de Weber-Fechner qui démontre que l’oreille humaine présente une relation logarithmique entre la grandeur physique du stimulus et sa perception physiologique, ainsi que l’analyse tirées de comparaisons auditives reproductibles, il apparaît que généralement la percpetion de l’intensité sonore d’un bruit est doublée quand le niveau d’intensité sonore augmente de 10 phon.