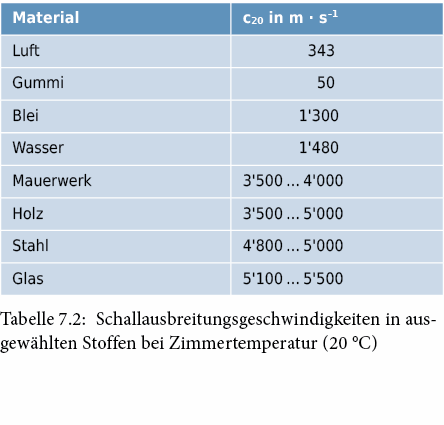
Unter Schall verstehen wir Schwingungen und deren Ausbreitung als Longitudinalwellen in einem elastischen Medium. Die in Schwingung versetzten Teilchen bewegen sich in Ausbreitungsrichtung vor und zurück.
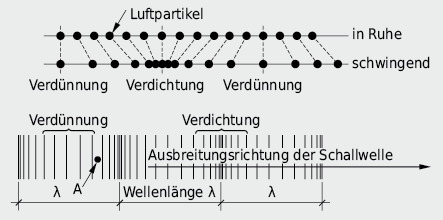
Die so aufgebauten Druckschwankungen können sich sowohl in festen Körpern als sog. Körperschall wie auch in der Luft als Luftschall ausbreiten. Akustische Signale, die das menschliche Ohr als Schall oder Schalldruck wahrnimmt, sind kleine Luftdruckschwankungen, die dem atmosphärischen Luftdruck (Barometerdruck) überlagert sind.
Solche Druckschwankungen stellen eine Störung des elastischen Mediums dar und breiten sich als Schallwellen mit einer dem Medium charakteristischen Geschwindigkeit, der Schallgeschwindigkeit c, aus. Als Näherung für die Schallgeschwindigkeit c in der Luft kann folgende Formel verwendet werden:


In festen Körpern kann in grober Näherung angenommen werden:


Die Zahl der Schwingungen eines Materieteilchens je Sekunde wird als Frequenz f (Schwingungszahl 1 s–1 ≙ 1 Hz) bezeichnet.

Die minimale Entfernung zweier Teilchen, die sich in demselben Schwingungszustand befinden, heisst Wellenlänge λ in m.
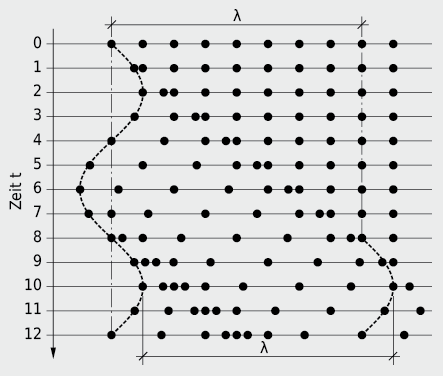
Der Zusammenhang zwischen den räumlichen und zeitlichen Druckzuständen bei der Ausbreitung des Schalles wird durch die Wellengleichung dargestellt. Bei einer ungedämpften, ebenen, harmonischen Welle lautet die Lösung der Wellengleichung:
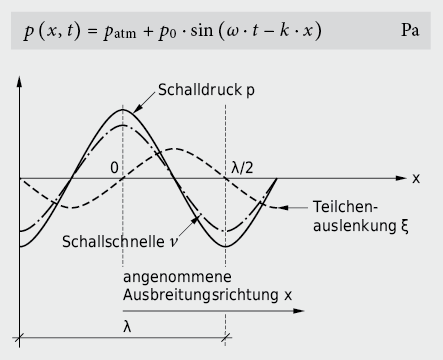
Mit 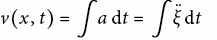 folgt:
folgt:
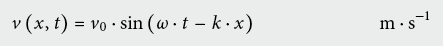

Zwischen Ausbreitungsgeschwindigkeit c, Frequenz f und Wellenlänge λ einer Welle besteht folgender grundlegender Zusammenhang:

Bei der Ausbreitung einer Welle durch verschiedene Medien bleibt die Frequenz f unverändert, hingegen ändern sich an der Mediengrenze Ausbreitungsgeschwindigkeit c und Wellenlänge λ.
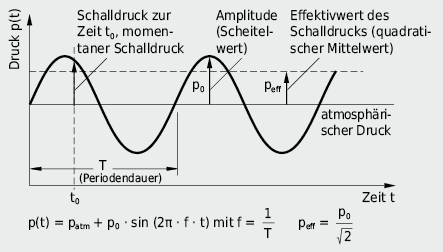
Schallaufnehmer zeigen nicht den momentanen Schalldruck p(t), sondern – analog zum Wechselstrom – den Effektivwert des Schalldrucks peff als zeitlichen quadratischen Mittelwert des momentanen Schalldruckes p(t). Er ist wie folgt definiert:
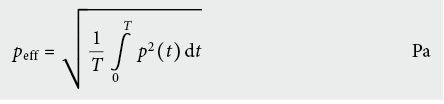
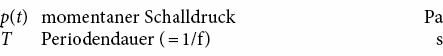
Für eine idealisierte, sinusförmige Druckschwankung gilt somit:

Der Dynamikbereich des Effektivwertes peff , innerhalb dessen das menschliche Ohr Luftdruckschwankungen als Schall wahrnehmen kann, ist sehr gross:

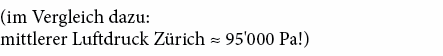
Im Gegensatz zur Schallgeschwindigkeit c, welche die Ausbreitung einer Druckwelle von Teilchen zu Teilchen beschreibt, versteht man unter der Schallschnelle v die Geschwindigkeit, mit der das einzelne Materieteilchen im Schallfeld um seine Ruhelage schwingt. Im Vergleich zur Schallgeschwindigkeit ist die Schallschnelle sehr klein. Schalldruck und Schallschnelle sind zueinander proportional, ihr Verhältnis ist orts- und zeitunabhängig.

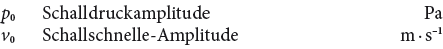
Dieses Verhältnis zwischen auslösender Ursache (Druck) und hervorgerufener Teilchengeschwindigkeit (Schallschnelle) wird als Schallkennimpedanz Z (Schallwiderstand) bezeichnet.

Die Grösse Z wird wegen des bestimmenden Einflusses auf die Reflexion von Schallwellen an Oberflächen/Grenzflächen (vgl. Abschnitt 7.2.1) auch Schallhärte genannt.
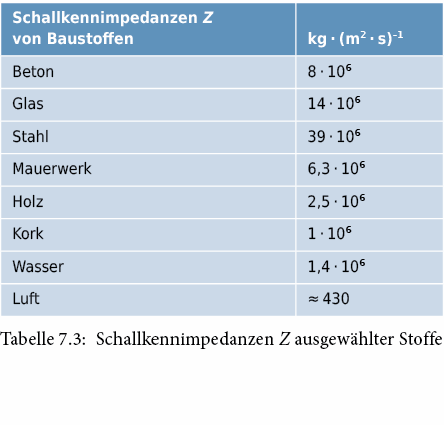
Diese etwas unanschauliche Grösse spielt eine wichtige Rolle bei der Beurteilung der Schalldämmung. Letztere ist um so besser, je unterschiedlicher die Schallimpedanzen zweier angrenzender Medien ausfallen. Daraus lässt sich jetzt schon die einfache Faustregel ableiten, dass man Luftschall mit schweren Körpern, Körperschall mit Luftzwischenräumen wirksam dämmen kann. Grenzen mehrere Stoffe gleicher Impedanz aneinander, so passiert der Schall ohne Schwächung.
Mit der sich ausbreitenden Welle wird im Schallfeld laufend mechanische Energie von der Erregerquelle abtransportiert und im Raum verteilt. Es ist daher sinnvoll, anstelle des Schalldruckes die Schallintensität I, d. h. die während der Zeitdauer dt durch ein Flächenelement ΔA hindurchtretende Schallenergie dW, zu verwenden.


Aufgrund des enorm breiten Arbeitsbereiches des menschlichen Ohres und dessen logarithmischer Verarbeitung physikalischer Schallreizsignale (Weber-Fechner-Gesetz) ist es nützlich, gewisse Kenngrössen des Schallfeldes im logarithmischen Massstab zu erfassen (vgl. Abb. 7.5). So sind die Schalldruckpegel Lp und der Schallintensitätspegel LI wie folgt definiert:
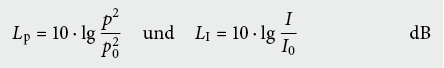

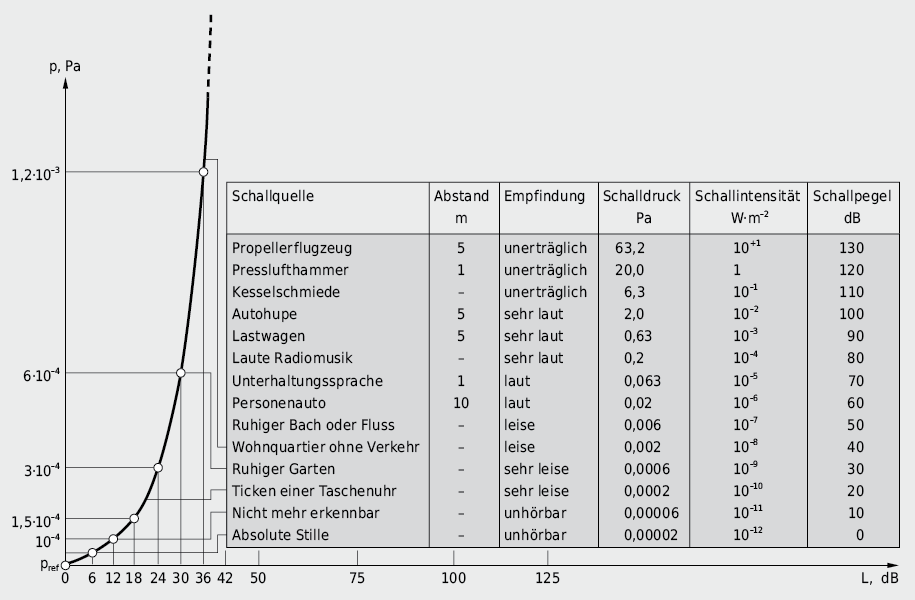
Der so definierte Schallintensität- bzw. Schalldruckpegel ist streng genommen eine dimensionslose Grösse. Die Einheit Dezibel (dB) wird – zur Bezeichnung der verwendeten Rechenvorschrift – einfach angefügt. Die logarithmische Definition reduziert den riesigen Bereich der hörbaren Intensitäten von etwa 12 Zehnerpotenzen auf eine Skala mit 120 dB-Stufen. Der Schallpegel ist eine relative Grösse, die mit Bezug auf ein Referenzniveau I0 resp. p0 bestimmt wird. Der Schalldruck p0 resp. der Schalldruckpegel 0 dB entspricht etwa dem Pegel an der Hörschwelle.
Zur Beschreibung von Schallquellen und ihrer Schallemissionen wird die Schalleistung beigezogen, die in Anlehnung an die oben definierten Schallpegel ebenfalls logarithmisch durch den sog. Schallleistungspegel Lw, mit einer Bezugsschallleistung P0 , beschrieben wird:

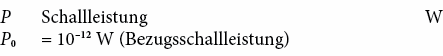
Die letzten beiden Grössen sind invariant gegenüber den akustischen Eigenschaften der Umgebung der Schallquelle und gegenüber der Art der Ausbreitung der Schallenergie.
Pegeladdition
Zwei Schallpegel werden « intensitätsmässig » addiert und nicht algebraisch in dB!
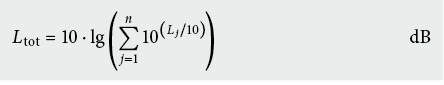
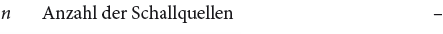
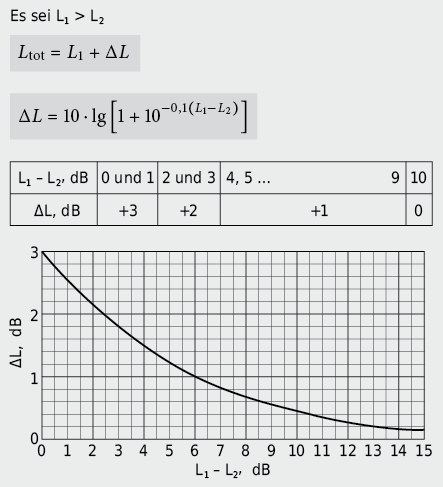
Die Pegeladdition zweier Einzelpegel zeigt eine maximale Erhöhung von 3 dB, falls die beiden zu addierenden Pegel gleich gross sind. Mit zunehmendem Unterschied der zu addierenden Pegel wird die « additive » Erhöhung des grösseren der beiden Pegel immer geringer; bei einem Pegelunterschied von 10 dB beträgt die « Additionskorrektur » nur noch 0,4 dB.
Die Addition von zwei Schallpegeln L1, L2 kann vereinfacht wie folgt geschehen:
Vielfach wird ein zeitlicher Mittelwert zur Beschreibung eines Schallereignisses benutzt. Der Mittelungspegel Leq , auch energieäquivalenter Dauerschallpegel genannt, ist wie folgt definiert:
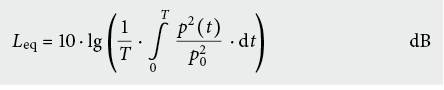

Schallwellen, die im Gehör auftreffen erzeugen eine Schallempfindung. Man unterscheidet bei dieser Schallempfindung zwischen Tonhöhe, Klangfarbe und Lautstärke.
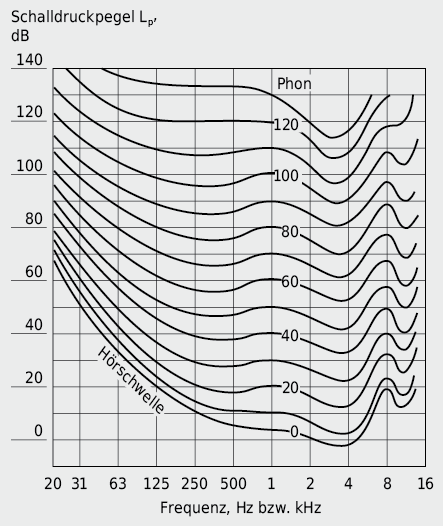
Das menschliche Ohr nimmt Geräusche im Frequenzbereich von etwa 16 bis 16’000 Hz wahr, wobei die Empfindlichkeit sowohl von Frequenz wie Intensität des einfallenden Schalles abhängt.
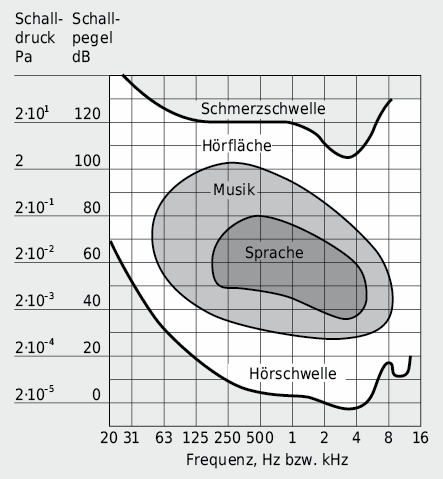
Der Bereich zwischen den kleinsten, noch wahrnehmbaren Schallpegeln (Hörschwelle) und den aufnehmbaren maximalen Pegeln (Schmerzschwelle) wird als Hörfläche bezeichnet. Bei ca. 1000 Hz liegt die Hörschwelle bei ca. 0 dB und nimmt für tiefe Frequenzen bis auf 70 dB zu. Die 1000-Hz-Schmerzschwelle liegt bei ca. 120 dB.
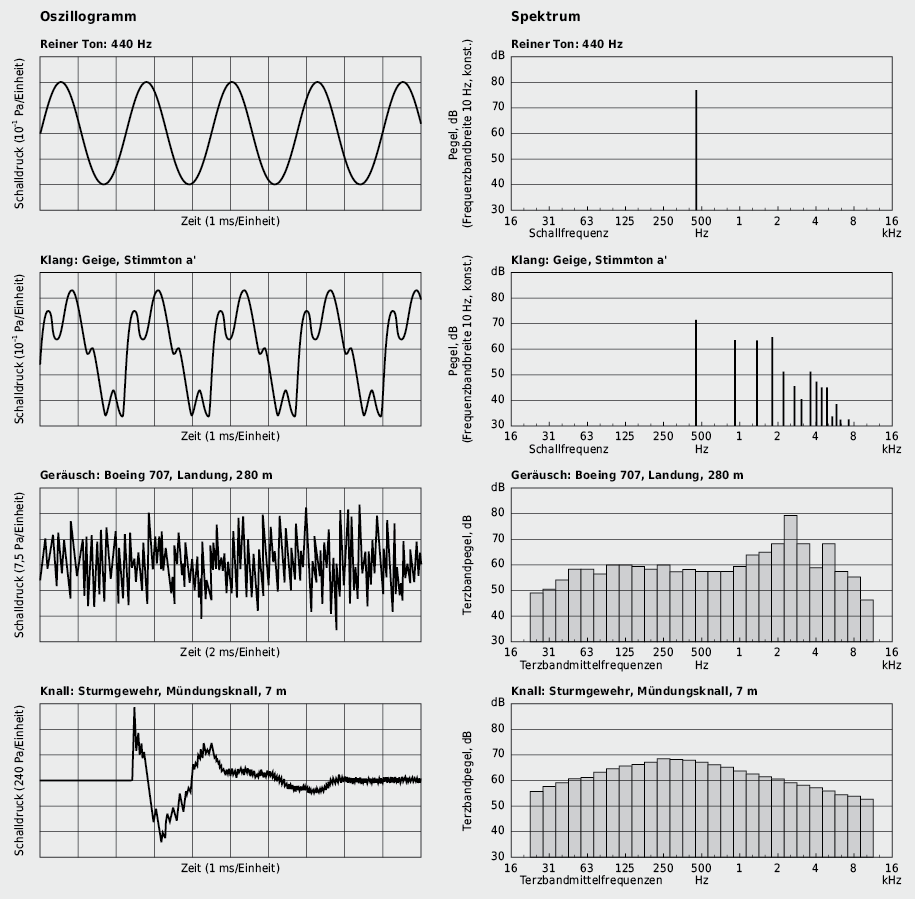
Somit genügt es nicht, ein Geräusch (Lärm) nur durch den zeitlichen Verlauf des Schallpegels zu beschreiben; vielmehr sind detaillierte Informationen über die Verteilung und die Stärke der in einem Geräusch auftretenden Frequenzen notwendig. Die sog. Frequenzanalyse liefert aus dem zeitlichen Verlauf des Schalldruckes die Verteilung der Schallintensitäten in einem beliebigen akustischen Signal als Funktion der Frequenz (→ Frequenzspektrum, vgl. Abb. 7.8, 7.9).
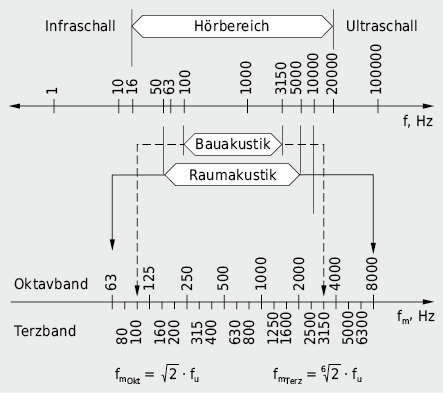
Bei der Darstellung des Amplituden-Frequenzspektrums wird der gesamte interessierende Frequenzbereich (ca. 16 Hz–16 kHz) mittels Bandfiltern, die jeweils nur einen scharf begrenzten Frequenzbereich durchlassen, in einzelne Bänder unterteilt. In der Regel erfolgt eine logarithmische Unterteilung, die bei Verdichtung des Frequenzbereiches mit einer gleichmässigen Auflösung eine grössere Übersichtlichkeit gewährleistet.
Bei der Oktavbandanalyse stehen die Randfrequenzen (untere Bandgrenze (fu), obere (fo)) zueinander im Verhältnis 1:2, bei der feineren Terzbandanalyse (1/3-Oktavband-Analyse) ist 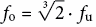 .
.
Der für den Schallschutz im Bauwesen wichtigste Frequenzbereich liegt etwa zwischen 100 Hz und 3200 Hz (ein Bereich, in dem das menschliche Ohr am empfindlichsten und der Lautstärkeanteil normaler Geräusche am grössten ist; vgl. Abb. 7.10).
Bei der Untersuchung von akustischen Systemen wird häufig das sogenannte weisse Rauschen verwendet. Bei diesem Geräusch ist die Leistungsdichte dl/df konstant. Bei Oktavfilterung nimmt der Pegel um 3 dB je Oktav, bei der Terzfilterung um 1 dB je Terz zu.
Bei bauakustischen Untersuchungen wird das rosa Rauschen zugezogen. Beim rosa Rauschen nimmt die Intensitätsdichte mit steigender Frequenz ab. Eine Oktav- oder Terzbandanalyse zeigt in jedem Band den gleichen Pegel.
Töne verschiedener Frequenz, aber mit gleichem Schalldruckpegel werden vom Menschen nicht als gleich laut empfunden. Der objektive Schalldruckpegel L in dB genügt deshalb nicht, um ein Geräusch hinsichtlich seiner subjektiven Wirkung zu charakterisieren. Die sog. Lautstärke beschreibt die Schallpegel gleich laut empfundener Töne unterschiedlicher Frequenz (vgl. Abb. 7.11).
Kurven gleicher Lautstärkepegel LS in phon geben für reine Töne jene Schallpegel an, die bei der entsprechenden Frequenz gleich laut empfunden werden wie ein 1000-Hz-Ton von bestimmtem Schalldruck.
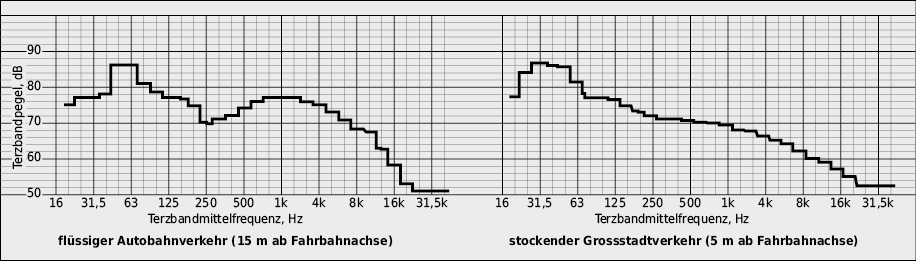
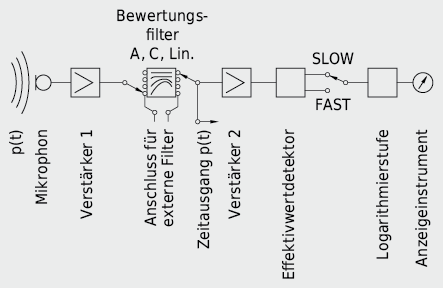
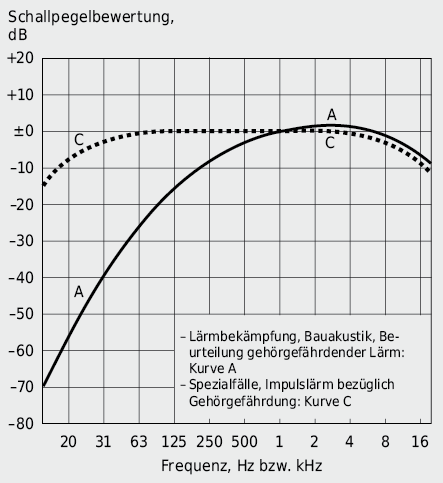
Um die Schallmessung dem menschlichen Schallempfinden anzupassen, müssen die Messwerte in den verschiedenen Frequenzbereichen entsprechend korrigiert werden. Den Messgeräten werden dabei Bewertungsfilter zugeschaltet, die entsprechend den Frequenzbewertungskurven (vgl. Abb. 7.12 und 7.13) das Signal abschwächen oder verstärken.
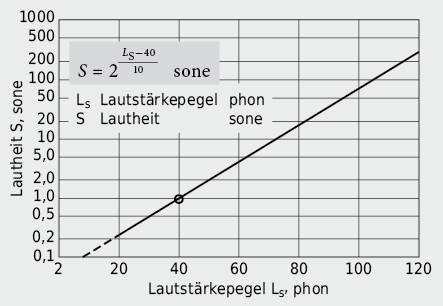
Diese für den praktischen Gebrauch z. T. unhandlichen, komplizierten Zusammenhänge um die Lautstärkewahrnehmung lassen sich vereinfachen, wenn die subjektive Lautstärkeempfindung nicht anhand des Lautstärkepegels LS phon, sondern durch die sog. Lautheit S sone beschrieben wird. Mit Hilfe des Weber-Fechner ’schen Gesetzes, das beim menschlichen Ohr einen logarithmischen Zusammenhang zwischen der physikalischen Reizgrösse und der physiologischen Reizwahrnehmung aufzeigt, und aus der Analyse reproduzierbarer Hörvergleiche lässt sich folgern, dass sich im Allgemeinen die Lautstärkewahrnehmung eines Geräusches verdoppelt, wenn sein Lautstärkepegel um 10 phon zunimmt.