7.2.1 Absorption, Reflexion, Dissipation
Die Gesetze der geometrischen Optik (Strahlenoptik) sind auch in der Akustik anwendbar, wenn die Dimension d ebener Objekte, die von der Schallwelle getroffen werden, grösser ist als die Wellenlänge des Schalles (d >> λ).
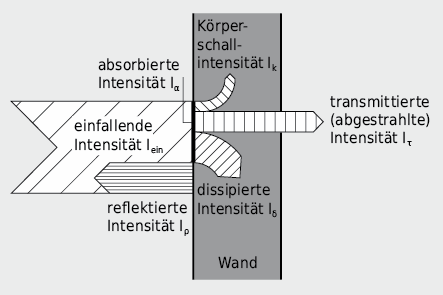
So wird z. B. ein Teil der Energie der einfallenden Welle an der Grenzfläche Luft/Festkörper reflektiert.
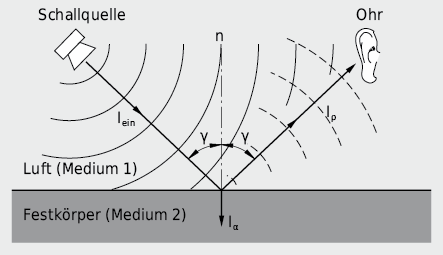
Zwischen auftreffender und reflektierter Welle entsteht eine Phasendifferenz, die mit abnehmender Schallkennimpedanz der Wand zunimmt. An schallharten Wänden (Schallschnelle → 0) tritt bei senkrechter Inzidenz eine Druckverdoppelung auf (keine Phasendifferenz). Bei extrem schallweichen Wänden (Schalldruck → 0) hingegen resultiert aus der Phasenumkehr eine Verdoppelung der Schallschnelle. Stimmen Wandimpedanz und Wellenwiderstand der Luft überein, so tritt keine reflektierte Welle auf, d. h., die Schallenergie geht in die Wand über und wird dort absorbiert.


In geschlossenen Räumen werden Schallwellen an den Wänden z. T. mehrmals reflektiert, sodass bei ungenügender Schallabsorption der Wandoberfläche aufgrund der Laufzeiten der einzelnen Schallwellen ein Nachhall entsteht, der die Verständlichkeit und Klangfarbe eventuell störend beeinflusst.
Sind die Dimensionen von beliebig orientierten Oberflächenrauhigkeiten grösser als die Wellenlänge des auftreffenden Schalles, so reflektieren die einzelnen Strukturflächen die einzelnen Wellenzüge nach allen möglichen Richtungen (diffuse Reflexion).
Die klassischen Ursachen für die Schallabsorption (Schalldämpfung) sind innere Reibung (hauptsächlich in porigen Stoffen wie Watte, Filz, Faserstoffen etc.) und Wärmeleitung. Beide Vorgänge tendieren zum lokalen Ausgleich der Unterschiede in der Geschwindigkeit (Impuls zwischen verschieden « schallschnellen » Molekülen) und der Temperatur (Wärmebewegung schallerregter Moleküle), entziehen also der Schallwelle Energie (Umwandlung in Wärmenergie: Dissipation) bzw. reduzieren deren Intensität. Massgebende Grösse zur Beschreibung der inneren Dämpfung ist der sog. Verlustgrad (Dissipationsgrad), der das Verhältnis der je Schwingungsperiode in Wärme überführten Schallenergie zur wiedergewinnbaren, mechanischen Schwingungsenergie angibt. Bei Baumaterialien liegen die Verlustgrade im Bereich von 10–3 bis 10–1: Beton, Backstein 10–3 bis 10–2 und Mineralfaserplatten (1–2) ∙ 10–1. Demzufolge ist die Dämpfung von Körperschall in festen Baustoffen normalerweise sehr gering:
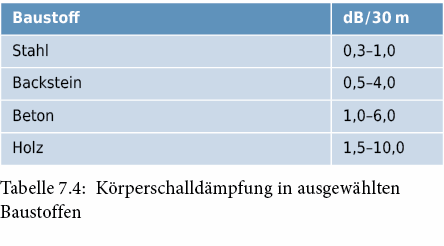
Durch die Anordnung absorbierender Beläge an Böden, Wänden und Decken der Räume lässt sich die Intensität der reflektierten Wellen reduzieren. Der Schallpegel sinkt, und der Nachhall wird verkürzt.
7.2.2 Resonanzeffekte
Werden schwingungsfähige Massen (« Resonatoren ») von aussen mit einer periodischen Kraft angeregt, so baut sich eine erzwungene Schwingung auf, und es kann der Fall eintreten, dass die Amplitude der angeregten Masse in einem bestimmten Bereich von Erregerfrequenzen extrem stark ansteigt (→ Resonanz).
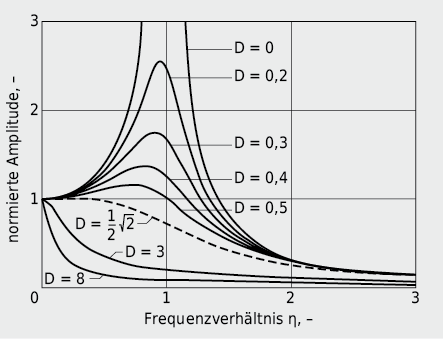
Anhand des Verhältnisses von Erreger- zu Eigenfrequenz (η = fE/f0) können drei grundlegend verschiedene Verhaltensweisen des Schwingers unterschieden werden:
- quasistationäre Anregung mit η ≈ 0,
- Resonanz mit η ≈ 1 und
- hochfrequente Anregung mit η >> 1.
Bei der sog. Resonanz liegt die Erregerfrequenz fE im Bereich der Eigenfrequenz f0 der angeregten Masse. Sowohl bei Luftschall als auch bei Körperschall sind bei der Schwingungsanregung analog den mechanischen Schwingvorgängen drei wesentliche Elemente beteiligt: Schwinger (Masse), Ankoppelung (Feder) und Dämpfer (Reibungselement). Alle derartigen Schwingsysteme haben ihren eigenen charakteristischen Resonanzbereich, der durch Masse, Feder und Dämpfer bestimmt wird.
Spuranpassung (Koinzidenzeffekt)
Bei schrägem Schalleinfall kann eine Wand im Takt der einfallenden Luftschallfrequenz fLuft verformt werden, und es entsteht in der Wand eine fortschreitende, transversale Spurwelle mit der Wellenlänge λSp. Andererseits können sich in biegeweichen Platten infolge örtlich begrenzter Körperschallerregung sog. freie Biegewellen der Wellenlänge λB ausbreiten. Den grossen seitlichen Auslenkungen, die für die Schallabstrahlung primär verantwortlich sind, stehen Spannungen und Dehnungen in Längsrichtung gegenüber.
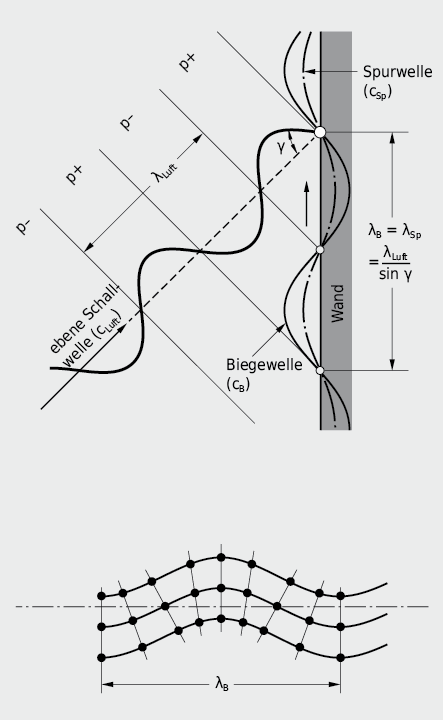
λB Wellenlänge Biegewelle
λLuft Wellenlänge Luftschallwelle
Diese Biegewellen zeigen im Gegensatz zu andern Körperschallwellen eine von der Frequenz abhängige Ausbreitungsgeschwindigkeit cB (Dispersion). Dabei spielt die Biegesteifigkeit pro Breite (B ‚ = E · I ‚ ) eine entscheidende Rolle:
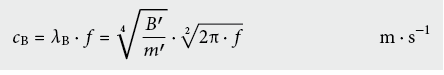

Eine Wandschale wird als biegesteif resp. biegeweich bezeichnet, wenn das Verhältnis B ‚ : m‘ gross bzw. klein ist.
Stimmen nun Wellenlänge λSp der Spurwelle (abhängig vom Einfallswinkel!) und λB der Biegewelle überein, so kommt es zu einer sog. räumlichen Resonanz, bei der die Schwingungsamplituden der Wand gross werden und der Schall die Wand praktisch ungehindert passiert (Koinzidenzeffekt, vgl. Abschnitt 7.4.2, Einschalige Konstruktionen).
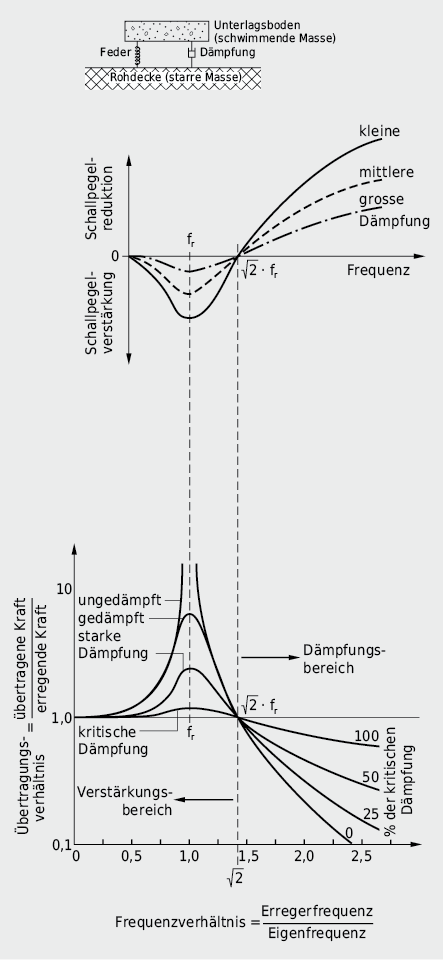
Zweimassenresonanz
Zweischalige Wand- und Deckensysteme können mechanisch als schwingfähiges Masse-Feder-Masse-System aufgefasst werden. Die beiden Schalen stellen die Massen dar, die Feder wird durch die trennende Luftschicht bzw. durch das zwischenliegende Dämpfungsmaterial gebildet.
Dieses Zweimassen-System zeigt bei Anregung im Bereich seiner Eigenfrequenz Resonanzeffekte, die dazu führen, dass die Dämmwirkung bei diesen Frequenzen zusammenfällt.
7.2.3 Beugung
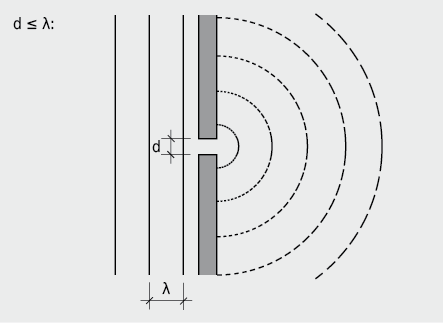
Ist die Dimension d von Hindernissen oder Öffnungen in der Schallausbreitungszone kleiner oder vergleichbar mit der Schallwellenlänge (d ≤ λ), so treten Beugungserscheinungen auf, die durch das Prinzip von Huygens beschrieben werden können («Eine Welle breitet sich so aus, dass jeder Punkt, den sie erreicht, selbst zum Zentrum einer neuen Welle, z. B. Kugelwelle, Zylinderwelle, wird.»).
Sind hingegen die Abmessungen des Hindernisses grösser als die Wellenlänge der auftreffenden Schallwelle (d > λ), so kommt es zur Ausbildung eines Schallschattens.
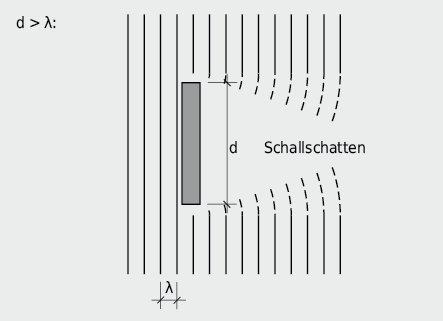
Beugungseffekte sind stark frequenzabhängig. Bei grosser Wellenlänge λ, gemessen an d, ist der «Schallschatten» in Abb 7.21 praktisch nicht vorhanden, bei kleinem λ ist er grösser.