7.2.1 Absorption, réflexion, dissipation
Les lois de l’optique géométrique (optique des rayons) sont aussi utilisables en acoustique quand la dimension d des objets plans rencontrés par les ondes sonores est plus grande que leurs longueurs d’onde (d >> λ).
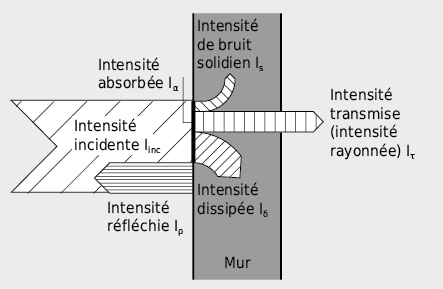
Ainsi, par exemple, une partie de l’énergie d’une onde incidente sur un interface entre l’air et un objet solide est réfléchie.
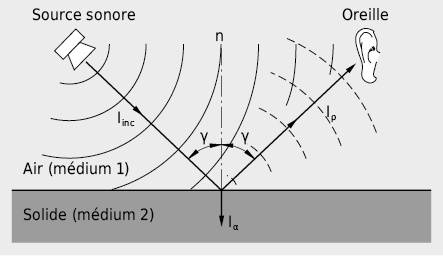
Entre l’onde incidente et l’onde réfléchie apparaît une différence de phase qui augmente avec la diminution de l’impédance acoustique caractéristique de la paroi. Sur les parois acoustiquement rigides (vitesse acoustique des particules → 0) un doublement de la pression apparaît lorsque l’incidence est normale (pas de différence de phase). Par contre, pour les parois acoustiquement très flexibles (pression acoustique → 0), un doublement de la vitesse des particules résulte du retournement de phase. Quand l’impédance de la paroi et la résistance aux ondes de l’air correspondent, il n’apparaît pas d’onde réfléchie ce qui signifie que l’énergie sonore pénètre dans la paroi et y sera absorbée.

Attention: les coefficients de réflexion et d’absorption doivent être clairement distingués des facteurs de réflexion et de transmission ( «coefficient de »: rapport d’intensités; «facteur de »: rapport d’amplitudes)
Dans les pièces fermées, les ondes sonores se réfléchissent en partie de nombreuses fois. Quand il n’y a pas assez d’absorption acoustique sur les surfaces des parois, ceci produit une réverbération due aux temps de vol des ondes sonores qui peut éventuellement déteriorer l’intelligibilité et le timbre. Quand les dimensions des rugosités de surface d’orientation quelconque sont plus grandes que la longueur d’onde du son incident, chaque élément de surface réfléchit chaque train d’onde dans toutes les directions possibles (réflexion diffuse).
L’origine usuelle de l’absorption acoustique (amortissement acoustique) est le frottement interne (principalement dans les matériaux poreux comme la ouate, le feutre, les matériaux fibreux etc.) et la conduction de chaleur. Les deux processus tendent à égaliser localement les différences de vitesse (impulsion entre les molécules) et de température (transport de chaleur par les molécules) ce qui retire de l’énergie à l’onde acoustique (transformation en chaleur: dissipation) donc réduit son intensité. La grandeur déterminante pour décrire l’amortissement interne est ce que l’on appelle le taux d’amortissement (taux de dissipation) qui indique le rapport entre la part de l’énergie acoustique transformée en chaleur à chaque période d’oscillation et l’énergie vibratoire mécanique recyclable. Pour les matériaux de construction les taux d’amortissement se situent entre 10–3 et 10–1: béton, brique 10–3 à 10–2 et panneaux de fibres minérales (1–2) ∙ 10–1. Il en ressort que l’amortissement du son solidien est normalement très faible dans les matériaux solides:
La disposition de revêtements absorbants au sol, sur les parois et au plafond d’un local, permet de réduire l’intensité des ondes réfléchies. Le niveau sonore décroît et la réverbération est écourtée.
7.2.2 Effets de résonance
Si des masses oscillantes (« résonateurs ») sont activées de l’extérieur par une force périodique, une oscillation forcée se produit. L’amplitude des masses excitées peut alors considérablement augmenter pour des fréquences d’excitation situées dans une plage déterminée (→ résonance).
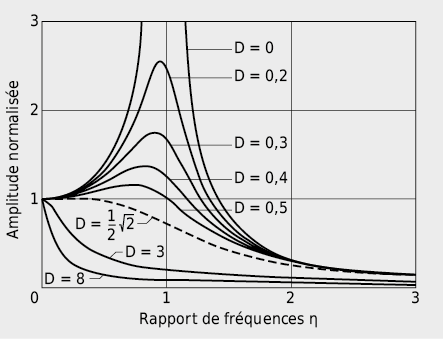
Selon le rapport entre la fréquence d’excitation et la fréquence propre (η = fE/f0), différents types de comportement du dispositif oscillant peuvent être distingués:
- excitation quasi stationnaire avec η ≈ 0,
- résonance avec η ≈ 1 et
- excitation à haute fréquence avec η>> 1.
Lorsqu’il y a résonance, la fréquence d’excitation fE se situe dans le domaine de la fréquence propre f0 de la masse excitée. Tant pour le son aérien que le son solidien, l’excitation oscillatoire comprend trois éléments principaux analogues aux oscillateurs mécaniques: oscillateur (masse), couplage (ressort) et amortisseur (élément de fottement). Tous les systèmes oscillants de ce type ont leur propre domaine de résonance caractéristique qui se détermine par une masse, un ressort et un amortisseur.
Effet de coïncidence
Avec un son à incidence oblique, une paroi peut se déformer au rythme correspondant à la fréquence fair de l’onde acoustique incidente. Une onde de flexion forcée progressive et transversale s’établit alors dans la paroi avec une longueur d’onde λSp. D’autre part, dans les panneaux flexibles, des ondes de flexion libre de longueur d’onde λB peuvent se propager suite à des excitations sonores solidiennes localisées. Les grands déplacements latéraux, qui sont les principaux responsables de la diffusion du son, induisent des contraintes et tensions qui se font face dans la direction longitudinale.
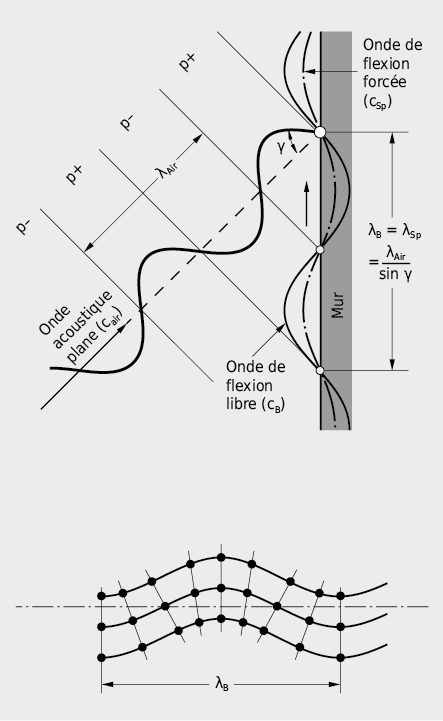
λB Longueur d’onde de l’onde de flexion
λair Longueur d’onde de l’onde acoustique dans l’air
Contrairement aux autres ondes acoustiques solidiennes, ces ondes de flexion ont des vitesses de propagation cB qui dépendent de la fréquence (dispersion). La rigidité à la flexion par unité de largeur (B ‘ = E · I ‘ ) joue là un rôle déterminant:
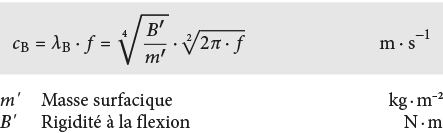
Une paroi est décrite comme rigide à la flexion ou flexible quand le rapport B ‘ : m’ est grand ou petit respectivement.
Lorsque la longueur d’onde λSp de l’onde de flexion forcée (qui dépend de l’angle d’incidence!) concorde avec la longueur d’onde λB de l’onde de flexion libre, il se produit ce que l’on appelle une résonance spatiale où les amplitudes des oscillations de la paroi deviennent grandes et où le son passe à travers l’élément pratiquement sans entrave (effet de coïncidence, voir section 7.4.2, éléments monocouches).
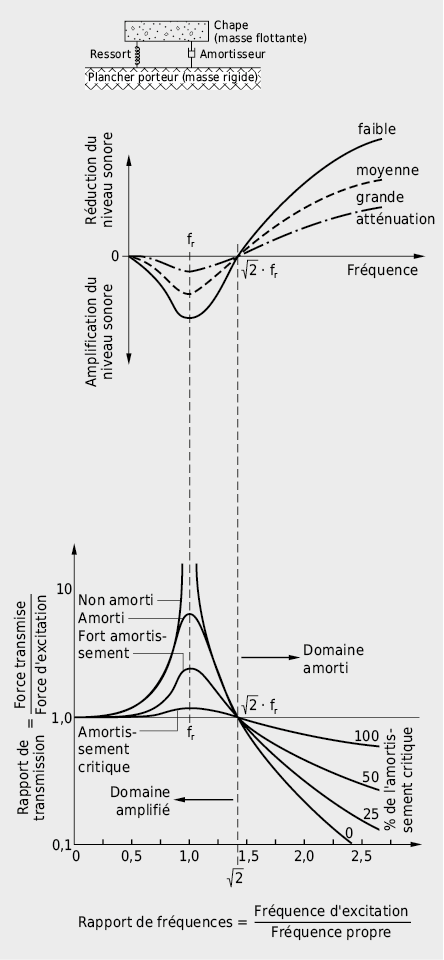
Résonance à deux masses
Les murs doubles et les systèmes de faux plafond peuvent être compris mécaniquement comme des systèmes oscillants masse-ressort-masse. Les deux couches représentent les masses alors que la couche d’air ou le matériau isolant qui les sépare correspond au ressort.
Un tel système à deux masses est sujet à un effet de résonance lorsque l’excitation se situe dans le domaine de sa fréquence propre ce qui conduit à un effondrement de l’effet d’amortissement pour ces fréquences.
7.2.3 Diffraction
Si la dimension d d’obstacles ou d’ouvertures dans la zone de propagation du son est plus petite ou comparable à la longueur d’onde (d ≤ λ), alors apparaissent des phénomènes de diffraction qui peuvent être décrits par le principe de Huygens («Une onde se propage de telle manière que chaque point qu’elle atteint devient lui même le centre d’une nouvelle onde, par exemple sphérique ou cylindrique.»).
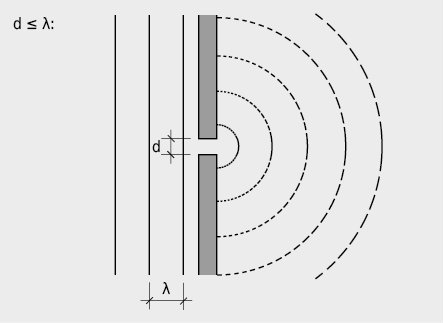
Quand au contraire les dimensions de l’obstacle sont plus grandes que la longueur d’onde des ondes sonores incidentes (d > λ), ceci conduit à la formation d’une ombre acoustique.
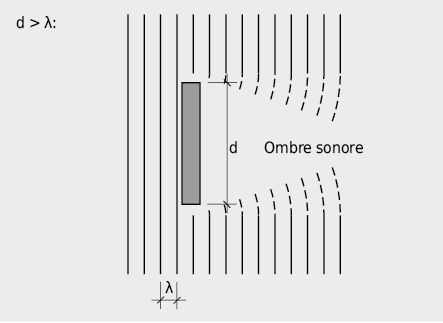
Les effets de diffraction dépendent fortement de la fréquence. Pour une grande longueur d’onde λ, relativement à d, « l’ombre acoustique » de la figure 7.21 n’apparaît pratiquement pas alors que pour de plus petites λ, elle est plus marquée.