9.2.1 Cercle, sphère et cylindre

9.2.2 Equation quadratique
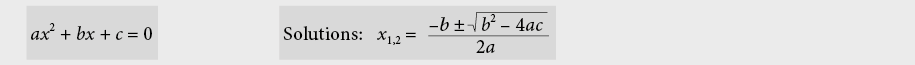
9.2.3 Identités remarquables
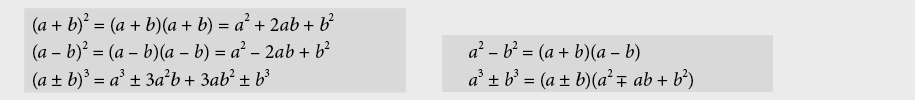
9.2.4 Fonction linéaire

9.2.5 Loi de puissance et fonctions puissances
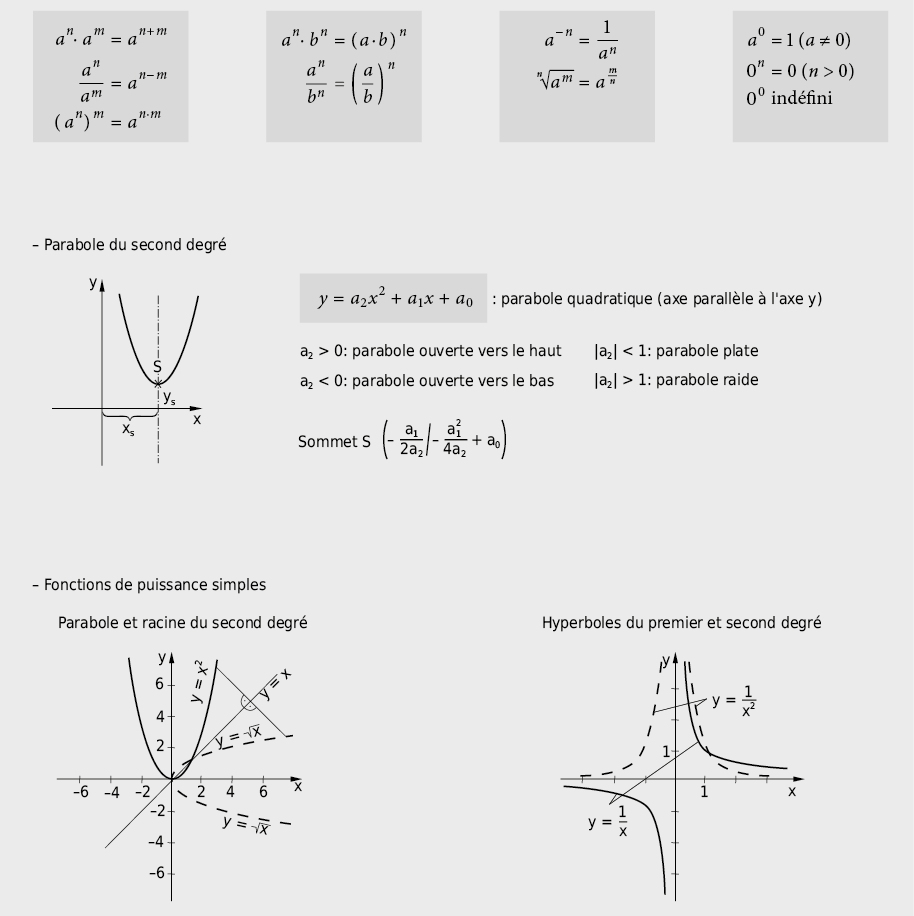
9.2.6 Loi du logarithme, fonctions logarithmiques et exponentielles
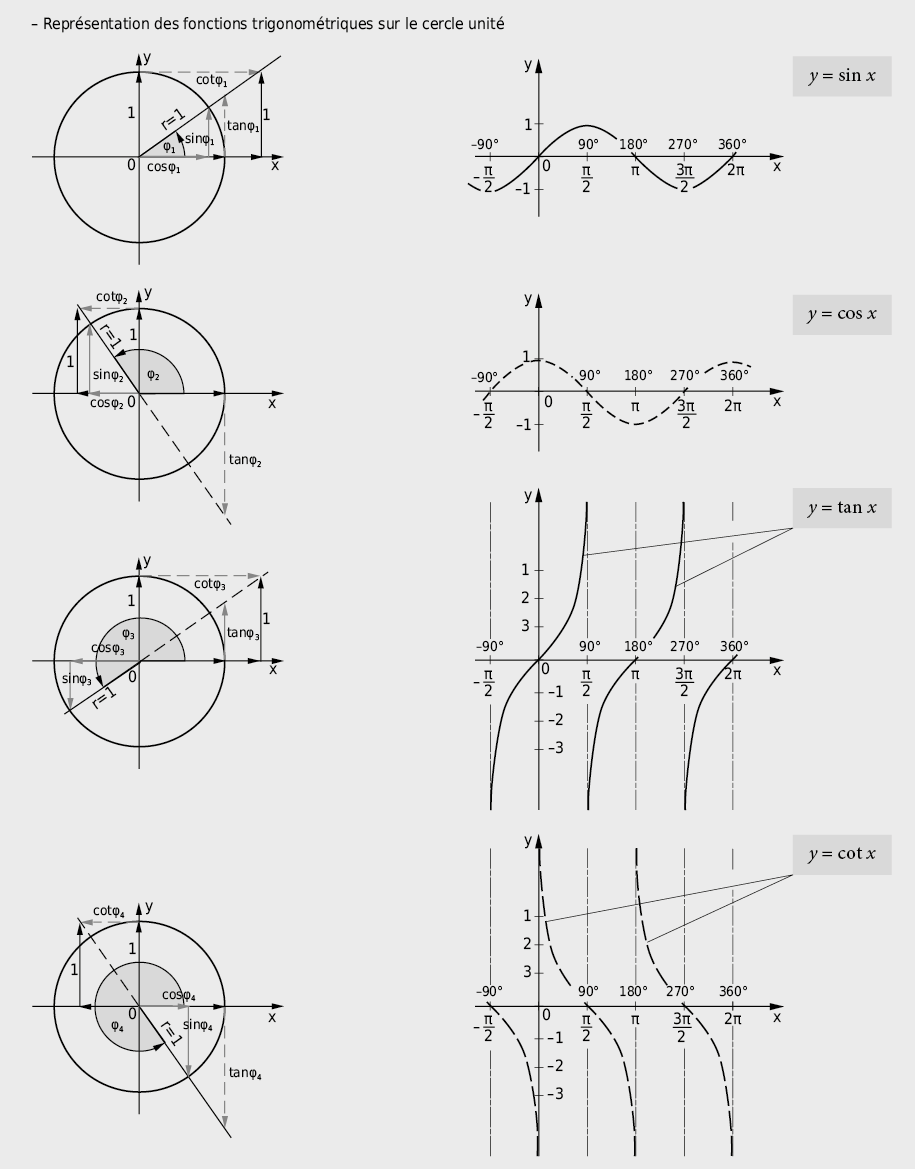
9.2.7 Triangles et fonctions trigonométriques


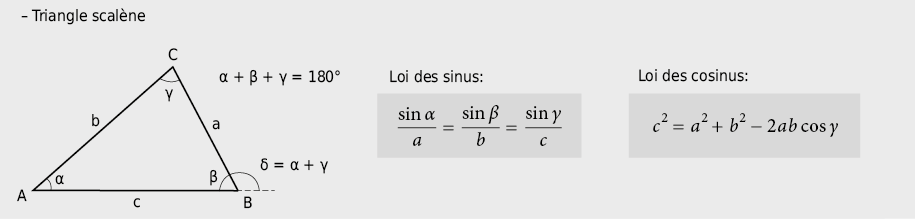
9.2.8 Dérivées et intégrales

9.2.9 Développements en séries

9.2.10 Produit vectoriel

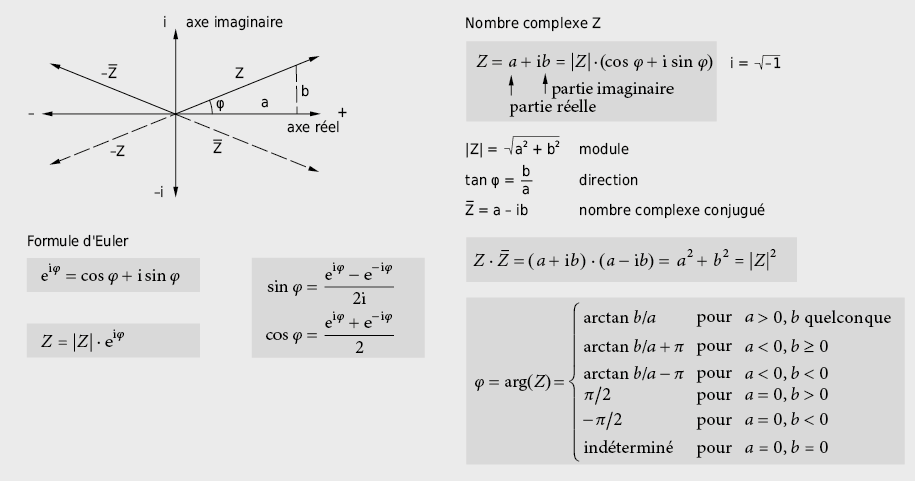
9.2.11 Nombres complexes
9.2.12 Les mesures et leur exploitation
Déjà dans la phase de planification des mesures, les lois de l’analyse d’erreur permettent de vérifier comment les incertitudes/marges d’erreur – systématiques et aléatoires – peuvent affecter les grandeurs mesurées. Avant la mesure on doit décider où, comment, à quel prix et avec quel but les erreurs peuvent ou doivent être réduites voire éliminées là où c’est possible.
Erreur aléatoire
Les fluctuations d’une valeur mesurée dues à des effets aléatoires sont décrites comme erreurs aléatoires (en anglais: random errors). Avec de telles erreurs, les grandeurs mesurées suivent généralement une distribution normale (distribution de Gauss).
Erreur moyenne d’une grandeur mesurée
Une grandeur µ est mesurée n fois sous des conditions aussi identiques que possible. Les n valeurs mesurées xj (j = 1 …n) forment un échantillon (en anglais: sample) d’un ensemble total (en anglais: population). Selon Gauss, la moyenne arithmétique x– (en anglais: arithmetic average) est la meilleure estimation (en anglais: estimate) de l’espérance µ (en anglais: expectation value, aussi appelée valeur la plus vraissemblable):

L’écart type s de l’échantillon (ISO: experimental standard deviation) ou son erreur moyenne vaut
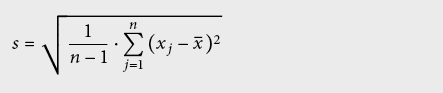
Il caractérise la précision de la procédure de mesure choisie et ne peut dès lors pas être amélioré en répétant les mesures; pour cela il faudrait changer de procédure de mesure.
Par contre, on peut diminuer l’incertitude statistique sur la valeur moyenne qui se dénomme écart type de la valeur moyenne sm (ISO: experimental standard deviation of the mean) en répétant les mesures:
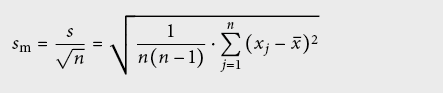
sm est une mesure de l’écart entre l’estimation x– et l’espérance µ.
Avec un petit nombre de mesures on peut difficilement déceler une distribution normale et l’estimation de l’espérance devient ainsi imprécise. La qualité de l’estimation doit alors être caractérisée par un intervalle de confiance (en anglais: range of confidence) autour de la moyenne arithmétique:
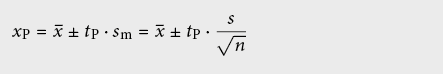
Le « facteur de confiance » tP dépend du nombre de répétitions de la mesure nw (nombre de mesures N moins nombre d’espérances k) et du niveau de confiance statistique P désiré (probabilité en %, que l’intervalle de confiance contienne la vraie valeur):
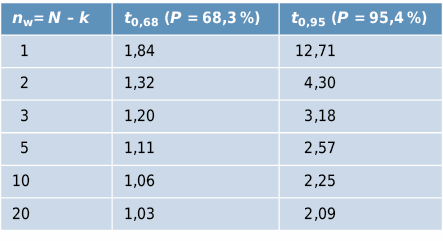
Propagation des erreurs avec plusieurs grandeurs mesurées
Si une grandeur physique f (x, y, z, …) ne peut pas être mesurée directement mais qu’elle doit être déterminée en mesurant d’autres variables x, y, z, … , alors sa valeur la plus vraisemblable se calcule à partir de la fonction appliquée aux valeurs moyennes des variables:

L’écart type s–f de la grandeur –f se calcule selon la loi de propagation des incertitudes de Gauss:
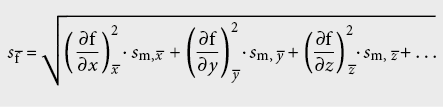
A l’aide des erreurs absolues ou relatives maximales des variables, l’ordre de grandeur de l’erreur peut être plus facilement estimé dans une première phase. Toutefois, on obtient de cette façon uniquement une estimation de l’erreur maximale:
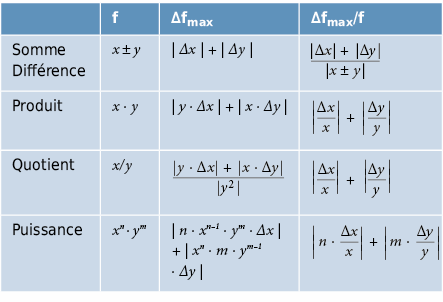
Erreur systématique
Ce genre d’erreurs de mesure (en anglais: systematic error) qui, malgré des conditions de mesure variables, prennent des valeurs toujours identiques – tant en terme d’échelle que de signe – ne peuvent pas être détectées ni réduites ou éliminées par des répétitions. Au mieux, elles peuvent être corrigées en modifiant la méthode de mesure.
Quand une incertitude de mesure systématique coexiste avec des erreurs aléatoires, l’incertitude totale doit être spécifiée comme la somme des incertitudes correspondantes.
Pour une fonction f = f (x, y, z, …), dont les variables sont affectées d’erreurs systématiques hj (j =x, y, z, …), l’erreur se propage de la façon suivante:
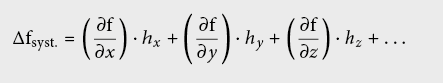
Contrairement aux erreurs aléatoires pour lesquelles les carrés des contributions des grandeurs mesurées s’additionnent comme des vecteurs orthogonaux, les erreurs systématiques doivent être additionnées algébriquement.
Ajustement par des relations fonctionnelles (analyse par régression)
Si l’on suppose une relation linéaire y = ax + b entre la variable x et la grandeur mesurée y, les paramètres de la pente (a) et de la valeur initiale (b) peuvent être déterminés par ajustement en employant la méthode des moindres carrés (en anglais: least square):
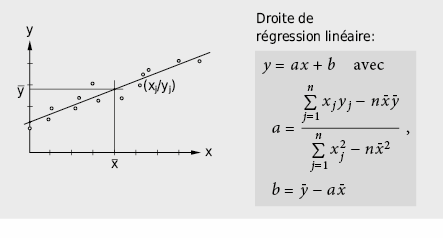
Souvent, une relation fonctionnelle non linéaire peut être linéarisée en procédant à une transformation de variables appropriée:
- les fonctions exponentielles par une simple représentation logarithmique (y → ln y)
- les fonctions puissances par une double représentation logarithmique (x → log x und y → log y)
Il est à noter que les facteurs de pondération gj de chaque valeur mesurée doivent être adaptés à la transformation.
Référence complémentaire sur ce thème
| [9.1] | W. H. Gränicher, Messung beendet – was nun? Einführung und Nachschlagewerk für Planung und Auswertung von Messungen, vdf Hochschulverlag AG an der ETH, Zürich (1996) |